Перейти к основному содержимому

Градиентный бустинг

Градиентный бустинг (gradient boosting [1], предложен в [2]) представляет собой приближение бустинга с использованием градиента функции потерь. В отличие от AdaBoost, он работает с произвольной дифференцируемой функцией потерь, а не только с экспоненциальной. В частности это позволяет решать не только задачу классификации, но и регрессии.

В качестве базовых моделей чаще всего используются решающие деревья небольшой глубины (gradient boosting over decision trees, GBDT).

Когда говорят о бустинге, то чаще всего имеют ввиду именно градиентный бустинг.

Идея метода​

Если отвлечься от множителя при базовой функции, то в бустинге решается задача подбора оптимальной fm+1(x)f_{m+1}(\mathbf{x}) такой, что

L(fm)=1N∑n=1NL(Gm(xn)+fm(xn),yn)→min⁡fm\mathcal{L}(f_{m})=\frac{1}{N}\sum_{n=1}^{N}\mathcal{L}\left(G_{m}(\mathbf{x}_{n})+f_{m}(\mathbf{x}_{n}),y_{n}\right)\to\min_{f_{m}}

Если вектор прогнозов функции [fm(x1),fm(x2),...fm(xN)]\left[f_{m}(\mathbf{x}_{1}),f_{m}(\mathbf{x}_{2}),...f_{m}(\mathbf{x}_{N})\right] заменить на вектор вещественных чисел u=[u1,u2,...uN]\mathbf{u}=[u_{1},u_{2},...u_{N}], то задача переформулируется в виде классической минимизации функции по аргументам:

L(u)=L(u1,...uN)=1N∑n=1NL(Gm(xn)+un,yn)→min⁡u1,u2,...uN\mathcal{L}(\mathbf{u})=\mathcal{L}(u_{1},...u_{N})=\frac{1}{N}\sum_{n=1}^{N}\mathcal{L}\left(G_{m}(\mathbf{x}_{n})+u_{n},y_{n}\right)\to\min_{u_{1},u_{2},...u_{N}}

Используя идеологию градиентного спуска, эту задачу в линейном приближении можно решить, положив

u1=−∂L(Gm(x1),y1)∂Gu2=−∂L(Gm(x2),y2)∂G⋯uN=−∂L(Gm(xN),yN)∂G\begin{aligned} u_{1} &= -\frac{\partial\mathcal{L}(G_{m}(\mathbf{x}_{1}),y_{1})}{\partial G} \\ u_{2} &= -\frac{\partial\mathcal{L}(G_{m}(\mathbf{x}_{2}),y_{2})}{\partial G} \\ & \cdots \\ u_{N} &= -\frac{\partial\mathcal{L}(G_{m}(\mathbf{x}_{N}),y_{N})}{\partial G} \\ \end{aligned}

Следовательно, в исходной постановке следует выбирать fm(x)f_{m}(\mathbf{x}) так, чтобы обеспечить

fm(x1)≈−∂L(Gm(x1),y1)∂Gfm(x2)≈−∂L(Gm(x2),y2)∂G⋯fm(xN)≈−∂L(Gm(xN),yN)∂G\begin{aligned} f_{m}(\mathbf{x}_{1}) &\approx -\frac{\partial\mathcal{L}(G_{m}(\mathbf{x}_{1}),y_{1})}{\partial G}\\ f_{m}(\mathbf{x}_{2}) &\approx -\frac{\partial\mathcal{L}(G_{m}(\mathbf{x}_{2}),y_{2})}{\partial G}\\ &\cdots \\ f_{m}(\mathbf{x}_{N}) &\approx -\frac{\partial\mathcal{L}(G_{m}(\mathbf{x}_{N}),y_{N})}{\partial G} \end{aligned}
Реализация

На практике это означает обучение fm(x)f_m(\mathbf{x}) на обучающей выборке:

{(x1,−∂L(Gm(x1),y1)∂G),(x2,−∂L(Gm(x2),y2)∂G),...(xN,−∂L(Gm(xN),yN)∂G)}\left\{ \left(\mathbf{x}_1,-\frac{\partial\mathcal{L}(G_{m}(\mathbf{x}_{1}),y_{1})}{\partial G}\right), \left(\mathbf{x}_2,-\frac{\partial\mathcal{L}(G_{m}(\mathbf{x}_{2}),y_{2})}{\partial G}\right), ... \left(\mathbf{x}_N,-\frac{\partial\mathcal{L}(G_{m}(\mathbf{x}_{N}),y_{N})}{\partial G}\right) \right\}

Алгоритм градиентного бустинга основан на итеративной оценке fm(x)f_m(\mathbf{x}) для m=1,2,...Mm=1,2,...M и добавлении этих функций к ансамблю Gm(x)G_m(\mathbf{x}).

Заметим, что в обучающей выборке для каждой базовой модели fmf_m вектора признаков будут одинаковыми, а целевые значения - разными, поскольку разными будут ошибки Gm(x)G_m(\mathbf{x}), уточняемой на каждой итерации.

Настройка fm(x)f_m(\mathbf{x}) происходит по правилу:

∑n=1N(fm(xn)+∂L(Gm−1(xn),yn)∂G)2→min⁡fm\sum_{n=1}^{N}\left(f_{m}(\mathbf{x}_{n})+\frac{\partial\mathcal{L}(G_{m-1}(\mathbf{x}_{n}),y_{n})}{\partial G}\right)^{2}\to\min_{f_{m}}

Заставить fm(x)f_m(\mathbf{x}) приближать антиградиент ансамбля можно, используя любую регрессионную функцию потерь. Квадратичные потери выше - просто наиболее типичный случай.

Тогда шагу градиентного спуска при минимизации L(u)\mathcal{L}(\mathbf{u})

u:=u−ε∇L(u)\mathbf{u}:=\mathbf{u}-\varepsilon\nabla\mathcal{L}(\mathbf{u})

будет приближённо соответствовать обновление ансамбля:

Gm(x):=Gm−1(x)+εfm(x),G_{m}(\mathbf{x}):=G_{m-1}(\mathbf{x})+\varepsilon f_{m}(\mathbf{x}),

где шаг обучения (learning rate) ε>0\varepsilon>0 выбирается пользователем (гиперпараметр).

Случай функции выигрыша

Если настройка ансамбля производится не минимизацией функции потерь, а максимизацией функции выигрыша, то fm(x)f_m(\mathbf{x}) нужно настраивать приближать не антиградиент потерь (градиент со знаком минус), а градиент функции (со знаком плюс).

Примеры​

Случай регресии​

Рассмотрим задачу регрессии y∈Ry\in\mathbb{R} с функцией потерь:

L(G,y)=12(G−y)2\mathcal{L}(G,y)=\frac{1}{2}\left(G-y\right)^{2}

Тогда следующая базовая модель будет настраиваться приближать

f(x)≈−∂L(G,y)∂G=−(G−y)=(y−G)f(\mathbf{x})\approx-\frac{\partial\mathcal{L}(G,y)}{\partial G}=-(G-y)=(y-G)

Обновление базовой модели пройдёт по правилу

Gm(xn):=Gm−1(xn)+εf(x)≈Gm−1(xn)+ε(yn−Gm−1(xn))\begin{aligned} G_{m}(\mathbf{x}_{n})&:=G_{m-1}(\mathbf{x}_{n})+\varepsilon f(\mathbf{x}) \\ & \approx G_{m-1}(\mathbf{x}_{n})+\varepsilon (y_{n}-G_{m-1}(\mathbf{x}_{n})) \end{aligned}

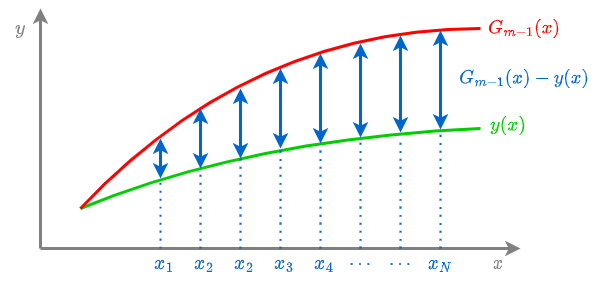
То есть в каждой точке xn\mathbf{x}_n ансамбль будет корректироваться на величину недопрогноза yn−Gm−1(xn)y_{n}-G_{m-1}(\mathbf{x}_{n}).

GB-regression.png

Случай бинарной классификации​

Для бинарной классификации y∈{+1,−1}y\in\{+1,-1\} зададим функцию потерь персептрона:

L(G,y)=max⁡{−Gy,0}\mathcal{L}(G,y) = \max\{-Gy,0\}

Тогда следующая базовая модель будет настраиваться приближать

fm(x)≈−∂L(G,y)∂G={y,Gy<00,Gy≥0f_{m}(\mathbf{x})\approx-\frac{\partial\mathcal{L}(G,y)}{\partial G}=\begin{cases} y, & Gy<0\\ 0, & Gy\ge0 \end{cases} Gm(xn):=Gm−1(xn)+εfm(x)≈Gm−1(xn)+{εyn,G(xn)yn≤00,G(xn)yn>0\begin{aligned} G_{m}(\mathbf{x}_{n})&:=G_{m-1}(\mathbf{x}_{n})+\varepsilon f_{m}(\mathbf{x}) \\ & \approx G_{m-1}(\mathbf{x}_{n})+\begin{cases} \varepsilon y_{n}, & G(\mathbf{x}_{n})y_{n} \le 0\\ 0, & G(\mathbf{x}_{n})y_{n}>0 \end{cases} \end{aligned}

В результате такого обновления ансамбль не изменяется для объектов, которые уже классифицируются корректно (G(xn)G(\mathbf{x}_{n}) и yny_{n} одного знака), и изменится на ε\varepsilon в сторону yny_n на неверно классифицированных объектах.

Это улучшает качество классификации неверно предсказанных объектов (повышает отступ), поскольку конечные прогнозы ансамбль выдаёт по правилу:

y^(x)={+1,Gm(x)>0,−1,Gm(x)<0.\hat{y}(\mathbf{x})= \begin{cases} +1, G_m(\mathbf{x})>0, \\ -1, G_m(\mathbf{x})<0. \end{cases}

Это изменение проиллюстрировано ниже:

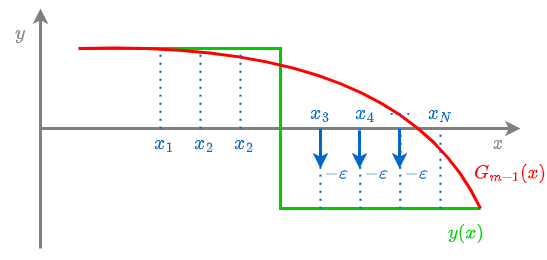
GB-classification.png

Как видим, при использовании функции потерь персептрона корректировка на ε\varepsilon осуществляется только для ошибочно классифицированных объектов, у которых y(x)y(\mathbf{x}) и Gm−1(x)G_{m-1}(\mathbf{x}) разных знаков.

Случай многоклассовой классификации​

Для многоклассовой классификации можно использовать методы один-против-одного, один-против-всех и коды, исправляющие ошибки, которые решают многоклассовую классификацию с помощью набора бинарных классификаторов.

Альтернативно можно решать многоклассовую классификацию напрямую. В этом случае Gm−1(x)∈RCG_{m-1}(\mathbf{x})\in\mathbb{R}^{C} будет представлять собой уже вектор из рейтингов для каждого из CC классов, а в качестве прогноза будет назначаться класс, обладающий максимальным рейтингом:

y^=arg⁡max⁡c∈{1,2,...C}Gm−1,c(x)\hat{y} = \arg\max_{c\in\{1,2,...C\}} G_{m-1,c}(\mathbf{x})

В случае минимизации потерь L(⋅)\mathcal{L}(\cdot):

fm(xn)≈−∂L(Gm−1(xn),yn)∂G∈RC,f_{m}(\mathbf{x}_{n})\approx-\frac{\partial\mathcal{L}(G_{m-1}(\mathbf{x}_{n}),y_{n})}{\partial G}\in\mathbb{R}^{C},

то есть базовая базовая модель и целевая величина будут представлять собой CC-мерные векторы, сближаемые через векторную функцию потерь.

Далее мы рассмотрим алгоритм бустинга в общем виде.

С частным случаем многоклассового бустинга при логистической функции потерь можно ознакомиться, например, в [3].

Литература​

  1. Wikipedia: gradient boosting.

  2. Friedman J. H. Greedy function approximation: a gradient boosting machine //Annals of statistics. – 2001. – С. 1189-1232.

  3. Мерков А. Б. Распознавание образов: введение в методы статистического обучения. // Москва: Едиториал УРСС. – 2019.