Перейти к основному содержимому

ROC-кривая

Управление готовностью назначать положительный класс​

Рассмотрим бинарный классификатор:

y^(x)=sign(g(x))={+1,g(x)≥0−1,g(x)<0\hat{y}(\mathbf{x}) = \text{sign}(g(\mathbf{x})) = \begin{cases} +1, & g(\mathbf{x})\ge 0 \\ -1, & g(\mathbf{x})< 0 \\ \end{cases}

Его относительная дискриминантная функция g(x)g(\mathbf{x}) характеризует степень уверенности классификатора в том, что объект принадлежит положительному классу.

Решающее правило можно обобщить, введя порог α\alpha, с которым производится сравнение:

y^(x)=sign(g(x)−α)={+1,g(x)≥α−1,g(x)<α\hat{y}(\mathbf{x}) = \text{sign}(g(\mathbf{x})-\alpha) = \begin{cases} +1, & g(\mathbf{x})\ge \alpha \\ -1, & g(\mathbf{x})< \alpha \\ \end{cases}

Чем α\alpha выше, тем более осторожно классификатор начинает предсказывать положительный класс для тех же самых объектов, и наоборот, для более низких α\alpha положительный класс назначается более охотно. Это полезный параметр чтобы управлять готовностью назначать объектам положительный класс без перенастройки самой модели.

Рассмотрим задачу кредитного скоринга, в которой для клиентов (объектов x\mathbf{x}) нужно предсказывать, вернут ли они кредит (y=+1)(y=+1) или нет (y=−1)(y=-1), на основе чего кредит либо выдаётся, либо нет. Для низких α\alpha мы более склонны давать кредиты, и это обосновано в периоды экономического подъёма. В периоды же экономического спада разумно выдавать кредиты более осторожно, повысив гиперпараметр α\alpha. Обратим внимание, что, варьируя порог α\alpha, мы можем управлять поведением модели в различных экономических ситуациях без необходимости перенастраивать модель.

Меры TPR и FPR​

Определим две меры качества бинарной классификации - true positive rate (TPR) и false positive rate (FPR):

TPR=TPN+,FPR=FPN−,TPR=\frac{TP}{N_+},\qquad FPR=\frac{FP}{N_-},

где N+,N−N_+,N_- - число объектов положительного и отрицательного класса соответственно. Мера TPR совпадает с ранее изученной мерой Recall. Также её называют recognition rate, поскольку по смыслу она характеризует долю верных (положительных) детекций среди объектов положительного класса. Меру FRP также называют false alarm rate, поскольку она характеризует долю неверных детекций (положительным классом) среди объектов отрицательного класса.

В примере с кредитным скорингом TPR будет измерять долю клиентов, которые могли бы вернуть кредит и мы действительно сочли их кредитоспособными. FPR же будет измерять долю клиентов, которые не способны вернуть кредит, но которых мы ошибочно сочли кредитоспособными.

ROC-кривая​

ROC-кривая (ROC-curve, receiver operating characteristic) показывает зависимость TPRTPR от FPRFPR при изменении порога α\alpha. Обе величины, измеряя частоты, изменяются от нуля до единицы по неубывающему закону, как показано на графике:

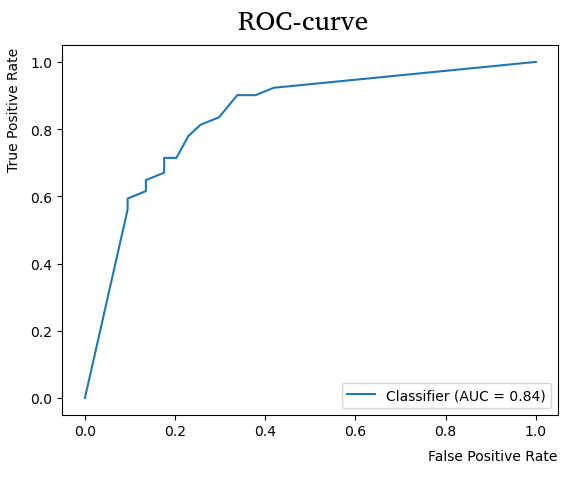
ROC-curve.png

При высоком α\alpha классификатор будет очень редко назначать положительный класс - только в тех случаях, когда он очень уверен в положительности класса. Тогда TPR будет близок к нулю (будет мало верно распознанных объектов положительного класса), как и FPR (поскольку положительный класс будет назначаться редко). Если же уменьшать α\alpha, то частота назначения положительного класса будет увеличиваться, увеличивая и TPR, и FPR, в результате чего мы прочертим ROC кривую.

Чем выше ROC-кривая, тем лучше классификатор, поскольку нам бы хотелось иметь более высокий TPR при том же уровне FPR.

ROC-кривая для случайного угадывания

Рассмотрим классификатор, который случайно назначает классы, независимо от вектора признаков x\mathbf{x}, по формуле

y^(x)=sign(ξ−α),\hat{y}(\mathbf{x})=\text{sign}(\xi-\alpha),

где ξ\xi - равномерно распределённая случайная величина на отрезке [0,1][0,1]. Докажите, что ROC-кривая, соответствующая этому классификатору будет прямая TPR=FPR. Существуют ли классификаторы, для которых ROC-кривая проходит ниже этой прямой? Можем ли мы извлечь пользу из таких классификаторов?

Агрегированной мерой качества классификации служит площадь под ROC-кривой, называемая AUC (area under curve).