Прогнозы на типичных и нетипичных объектах
Для отладки обученной модели полезно рассмотреть её обработку:
-
типичных объектов (прототипов, prototypes);
-
нетипичных объектов (критиков, criticisms).
Объекты-прототипы лежат в центрах плотно заполненных областей признакового пространства. Объекты-критики находятся, наоборот, в слабо заполненных областях пространства признаков.
Для простоты последующего анализа множество прототипов и критиков нужно выбирать минимально достаточным, т.е. с использованием минимального числа характерных примеров.
Пример выделения прототипов и критиков для двумерных данных показан ниже [1]:
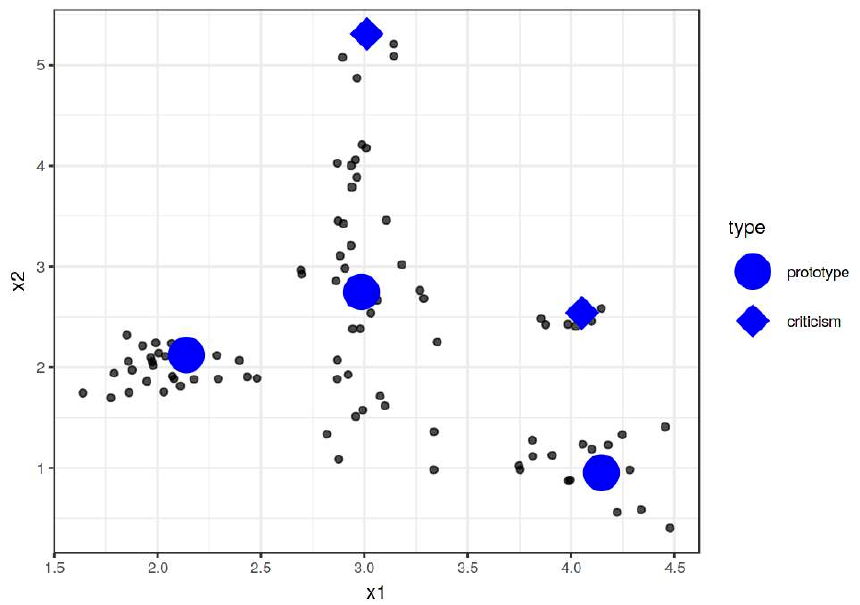
Как видим, прототипы лежат в областях сгущения характерных объектов, а критики - в сгущениях нетипичных объектов, что позволяет описать типичные и нетипичные случаи минимальным числом примеров!
Примеры объектов-прототипов и критиков для задачи определения породы собаки и распознавания рукописных цифр по фото показаны ниже [1]:

Видно, что прототипы первой задачи представляют собой классические фото собак крупным планом. Критики же представляют нетипичные случаи, где собак на фото может быть много, на собаку что-то одето и т.д.
Аналогично и во второй задаче - прототипы представляют собой классические и разборчивые написания цифр. На изо�бражениях-критиках цифры написаны неразборчиво, слишком жирно или вообще не соответствуют никакой цифре!
Поскольку прототипы и критики ёмко описывают множество типичных и нетипичных случаев, они позволяют легко получить комплексное представление о работе модели в разных сценариях перед её внедрением.
Прототипы можно найти как центры кластеров при кластеризации методом К-медоид [2]. Этот метод кластеризации аналогичен методу К-средних [3], только центрами могут выступать лишь объекты обучающей выборки. В качестве критиков можно выбирать объекты выборки, далёкие от центров кластеров, а также друг от друга.
Существует и более продвинутая процедура выделения прототипов и критиков - MMD-critic, описанная в [1] и имеющая реализацию на python [4].