Значения Шепли

Значения Шепли (Shapley values [1]) позволяют объяснить для выбранного объекта $\mathbf{x}$ вклад значения каждого признака в прогноз модели $f\left(\mathbf{x}\right)$. Оценка производится для конкретного объекта и конкретного значения выбранного признака. Вклад значений всех признаков и обеспечивает результирующий прогноз.

Рассмотрим в качестве примера задачу Titanic [2], в которой по описанию каждого пассажира (включающему класс билета, пол, возраст и т.д.) нужно предсказать, выжил он в результате кораблекрушения или нет. На рисунке ниже [3] показано объяснение прогнозируемой вероятности выживания для одного из пассажиров:

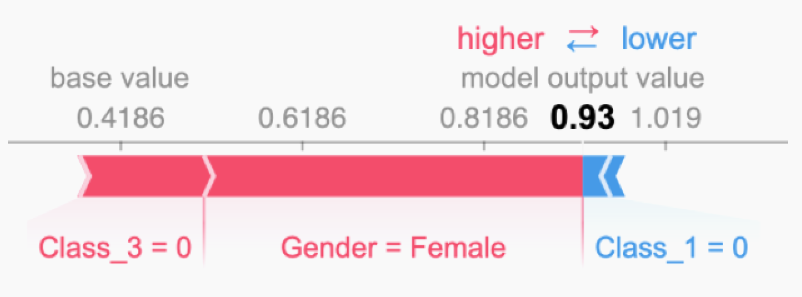
Видно, что высокая вероятность прогнозируемого выживания 0.93 обеспечивается тем, что пассажир - женщина, которая не путешествовала третьим классом. Однако то, что она не путешествовала первым классом (в one-hot кодировании индикаторы класса - разные признаки) несколько снизило оцениваемую вероятность выжить.

Псевдокод для приближённого расчёта значения Шепли, измеряющего вклад $j$-го признака в прогноз приведён ниже.

Результат: значение Шепли для значения $j$-го признака

Параметры: количество итераций $M$, исследуемый объект $\mathbf{x}$, индекс признака $j$, матрица данных $\mathbf{X}$, модель машинного обучения $f$.

1. Для всех $m = 1, \ldots, M$:

   • Выбрать случайный объект $\mathbf{z}$ из матрицы данных $\mathbf{X}$

   • Случайным образом выбрать перестановку $\mathbf{p}$ признаков

   • Упорядочить объект $\mathbf{x}$: $\mathbf{x}_{\mathbf{p}} = (x_{(1)}, \ldots, x_{(j)}, \ldots, x_{(D)})$

   • Упорядочить объект $\mathbf{z}$: $\mathbf{z}_{\mathbf{p}} = (z_{(1)}, \ldots, z_{(j)}, \ldots, z_{(D)})$

   • Построить два новых объекта:

     • С признаком $j$: $\mathbf{x}_{+j} = (x_{(1)}, \ldots, x_{(j-1)}, x_{(j)}, z_{(j+1)}, \ldots, z_{(D)})$
     • Без признака $j$: $\mathbf{x}_{-j} = (x_{(1)}, \ldots, x_{(j-1)}, z_{(j)}, z_{(j+1)}, \ldots, z_{(D)})$

   • Вычислить маржинальный вклад:

     $$\phi_j^{(m)} = f(\mathbf{x}_{+j}) - f(\mathbf{x}_{-j})$$

2. Вычислить значение Шепли как среднее маржинальных вкладов:

   $$\phi_j(\mathbf{x}) = \frac{1}{M} \sum_{m=1}^M \phi_j^{(m)}$$

Число повторов $M$ определяет точность полученной оценки: чем выше - тем она получится точнее.

По сути, происходит оценка, насколько в среднем вырастает прогноз, если оставить и заменить интересующее значение признака случайным значением из выборки при одновременной замене случайного подмножества других признаков. В итоге получим среднее изменение прогноза за счёт того, что интересующий признак принимает заданное значение.

Таким образом, значения Шепли оценивают важность признаков в контексте заданного объекта $\mathbf{x}$, а сумма их значений равна отклонению прогноза $f(\mathbf{x})$ от среднего прогноза по всем объектам.

Недостатком метода, как для перестановочной важности признаков, является усреднение по малореальным объектам, поскольку в процедуре оценки генерируются синтетические объекты, для которых часть значений признаков взята из одного объекта, а другая часть - из другого, что может приводить к маловероятным комбинациям признаков, особенно когда признаки сильно скоррелированы.

Глобальная важность признака

С помощью значений Шепли можно вычислить и глобальную важность признака. Для этого абсолютные значения Шепли для этого признака усредняются по всем объектам выборки:

$$\text{Importance}(j)=\frac{1}{N}\sum_{n=1}^N |\phi_j(\mathbf{x}_n)|$$

---

Детальнее о значениях Шепли, их теоретическом обосновании и свойствах можно прочитать в [4] и [5]. Пример практического расчёта этих значений в python, используя библиотеку shap, доступен в [6].

Литература

1. Wikipedia: Shapley value.

2. openml.org: Titanic dataset.

3. Gosiewska A., Biecek P. IBreakDown: Uncertainty of model explanations for non-additive predictive models //arXiv preprint arXiv:1903.11420. – 2019.

4. Molnar C. Interpretable machine learning. – Lulu. com, 2020: Shapley values.

5. Molnar C. Interpretable machine learning. – Lulu. com, 2020: SHAP.

6. Документация shap: an introduction to explainable AI with Shapley values.