Влияние обучающих объектов

Поскольку прогнозы строятся моделью, настроенной на некоторой обучающей выборке, то анализировать прогнозы сложных моделей можно, изучая наиболее сильно влияющие объекты выборки на прогноз (influential instances).

Например, на рисунке ниже (источник) виден один объект справа внизу, который оказывает наиболее сильное влияние на прогнозы модели, смещая их.

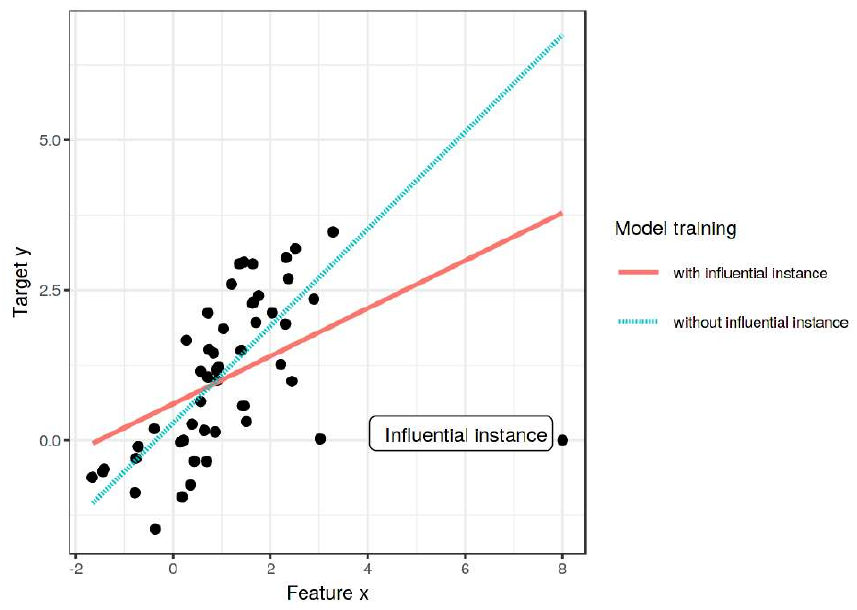
Это неправильная ситуация, когда всего лишь один или несколько объектов сильно влияют на прогнозы. Она свидетельствует о наличии выбросов в обучающей выборке, которые нужно отфильтровать.

Этот подход также позволяет бороться со специальным видом атак на модель, когда в обучающую выборку подмешивается небольшое число специальных наблюдений, искажающих прогнозы модели в нужную сторону (poisoning attack).

Определим влияние объектов более формально. Пусть предиктивная модель $f\left(\mathbf{x}\right)$ обучена на всех наблюдениях, а $f_{-i}\left(\mathbf{x}_{n}\right)$ обучена на всех, кроме $i$-го объекта $\left(\mathbf{x}_{i},y_{i}\right)$. Тогда влияние $i$-го наблюдения на прогноз объекта $\mathbf{x}$ можно оценить как

$$\text{influence}_{i}\left(\mathbf{x}\right)=\left|f\left(\mathbf{x}\right)-f_{-i}\left(\mathbf{x}\right)\right|,$$

а глобальное влияние на все прогнозы выборки будет получаться усреднением по объектам:

$$\text{influence}_{i}\left(X,Y\right)=\frac{1}{N}\sum_{n=1}^{N}\left|f\left(\mathbf{x}_{n}\right)-f_{-i}\left(\mathbf{x}_{n}\right)\right|$$

В случае векторного прогноза (например, вектор вероятностей классов) модуль в формулах нужно заменить на векторную норму от изменений.

Можно исключать объекты не по одному, а группами по определённому критерию. Например, по времени наблюдений. И анализировать, насколько модель зависит от более старых и более новых наблюдений. Или анализировать наблюдения, полученные из разных источников. Если источники равнозначны, то было бы странно ожидать, что наблюдения из определённого источника сильнее влияют на прогнозы, чем остальные.

При перепроверке измерений в первую очередь нужно перепроверять те объекты, которые сильнее всего оказывают влияние на прогноз. Также, если мы обучили модель на одной выборке, а применяем к другой, то можно анализировать несоответствие выборок. Например, мы обучили модель предсказывать скорость выздоровления от методик лечения на пациентах одной больницы, а применяем к другой. И выяснили, что самыми значимыми объектами будут более пожилые пациенты. Отсюда можно сделать вывод, что во второй больнице более возрастные пациенты, и именно для таких пациентов нужно собирать больше данных.

Оценив влияние $\text{infuence}_{i}\left(\mathbf{x}_{n}\right)$ для каждого объекта $\mathbf{x}_{n}$ обучающей выборки, можно построить простую интерпретируемую модель, которая будет предсказывать это влияние. Проще всего использовать дерево небольшой глубины. Анализируя структуру этого дерева, мы получим общее представление о тех характеристиках, которыми обладают значимые объекты. Например, в задаче с пациентами больницы мы можем понять, что самыми значимыми пациентами выступают пожилые пациенты с жалобами на боли в пояснице.

Если исключать объекты по одному, а не группами, то расчёты важности будут вычислительно трудоёмкими, поскольку предполагают, что для каждого объекта выборки нужно перенастраивать модель, когда этот объект в выборку включён и исключён. Эти расчёты упрощаются при использовании метода опорных векторов и регрессии опорных векторов, поскольку прогнозы для этих методов зависят только от опорных объектов (которых мало) и не зависят от неинформативных объектов (большинство).

Для нейросетей существует эффективный алгоритм приближённого расчёта важности объектов без многократной перенастройки модели с включением/исключением каждого объекта выборки (статья). В этой работе, в частности, рассматривается задача классификации изображений на собак и рыб, и для тестового изображения рыбы приводятся два самых значимых обучающих объекта для её классификации двумя моделями - методом опорных векторов с Гауссовым ядром (SVM-RBF) и нейросетевой моделью Inception V3.

Из иллюстрации видно, что метод SVM-RBF больше смотрит на попиксельное сходство между изображениями, игнорируя семантику, поскольку самые важные обучающие изображения оказались той же цветовой гаммы, но содержат рыб другой разновидности. А модель Inception концентрируется именно на семантической близости: самые важные обучающие объекты для неё отличаются по цветам, зато содержат фотографии рыбы того же самого вида, которую необходимо классифицировать.