Влияние признаков на качество прогнозов

Перестановочная важность признаков

Метод перестановочной важности признаков (permutation feature importance) представляет собой способ расчёта степени влияния каждого признака на прогнозы модели.

Достоинством метода является то, что он применим:

для любой модели (white-box, black-box models);
для любой задачи (классификация, регрессия и др.);
для любой функции потерь.

Пусть $X\in\mathbb{R}^{N\times D}$ - матрица объекты-признаки (вектора признаков для каждого объекта составляют строки этой матрицы), а $Y\in\mathbb{R}^{N}$ - вектор откликов для объектов в матрице $X$ . Пара $(X,Y)$ может соответствовать как обучающей, так и внешней валидационной выборке.

Пусть $L\left(f|X,Y\right)$ - потери модели на выборке $(X,Y)$ , например, средний модуль ошибки для регрессии или частота ошибок для классификации. Чтобы оценить важность $j$ -го признака, перемешаем (с возвращением) случайным образом значения этого признака (значения $j$ -го столбца матрицы $X$ ), получим новую матрицу $\widetilde{X}_{j}$ , отличную от $X$ только в $j$ -м столбце.

При таком случайном перемешивании общее распределение $j$ -го признака сохранится, но связь с $y$ потеряется. Пусть $L\left(f|\widetilde{X}_{j},Y\right)$ - потери модели на выборке $(\widetilde{X}_{j},Y)$ . Тогда перестановочная важность признака $j$ (permutation feature importance, PMI, [1], [2]) считается по одной из следующих формул:

\tag{1} \frac{L\left(f|\widetilde{X}_{j},Y\right)}{L\left(f|X,Y\right)}

\tag{2} L\left(f|\widetilde{X}_{j},Y\right)-L\left(f|X,Y\right)

Таким образом, перестановочная важность признака показывает, во сколько/на сколько средние потери прогнозов изменятся, если модель не сможет эффективно использовать информацию, хранящуюся в том или ином признаке.

Устойчивость к случайности

Обратим внимание, что результат зависит от случайной перестановки признака. При различных перестановках будем получать различный результат. Поэтому на практике статистика пересчитывается много раз для случайных перестановок, а в качестве итогового ответа выдаётся её среднее значение.

Пример расчёта важности признаков по формуле (1) для задачи bike sharing [3] приведён ниже [4], где точками обозначены средние значения важности при перезапусках метода, а интервал показывает нижнюю и верхнюю квантиль по значениям в различных запусках:

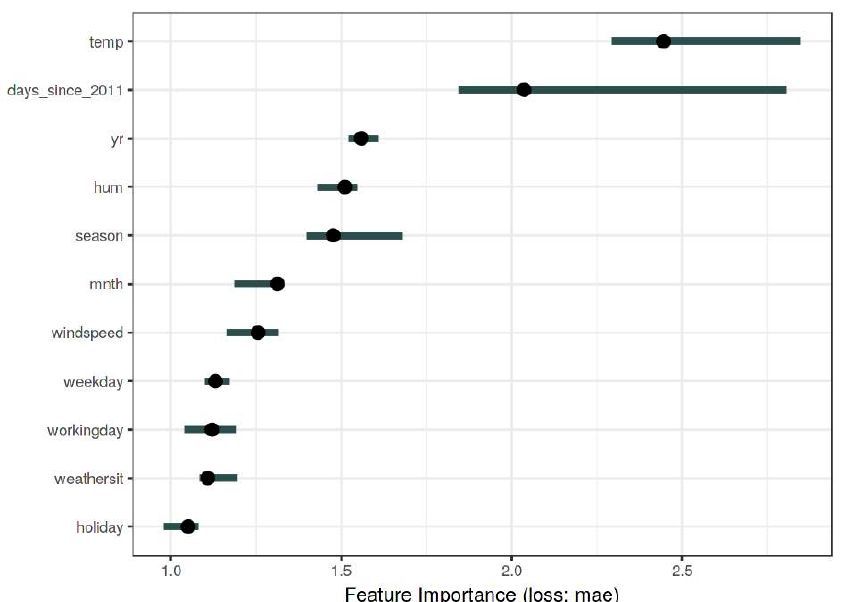
Как видим, все признаки оказывают значимое влияние на прогноз, кроме признака holiday, поскольку его доверительный интервал покрывает единицу.

Рекомендуется использовать отношение (1), а не разность потерь (2), поскольку тогда можно сопоставлять важность признаков на разных моделях с разными диапазонами потерь: относительное изменение потерь более инвариантно к изменению диапазона, чем разность.

Перестановочную важность признаков можно считать:

по обучающей выборке: тогда узнаем, на каких признаках модель сильнее всего переобучилась;
по валидационной тестовой выборке: тогда узнаем, какой признак важнее для прогнозирования новых объектов.

Достоинства

Метод даёт глобальную интерпретируемость для всей выборки в привязке к конкретной функции потерь. В этом её достоинство по сравнению с внешними эвристическими методами расчёта важности признаков, такими как корреляция [5] с откликом или нормализованная взаимная информация (normalized mutual information, NMI [6]), которые зависят от прогнозов и верных ответов, но никак не зависят от рассматриваемой функции потерь.

Недостатки

К недостаткам метода стоит отнести то, что расчёт важности будет во многом основываться на нереалистичных объектах.

Рассмотрим в качестве объектов пациентов больницы, у которых признаки включают рост и вес. Оценивая важность роста, мы переставляем значения роста случайным образом, оставляя вес таким, каким он был, что может приводить к малореальным пациентам с большим весом, но малого роста, и наоборот.

Также в случае связанных признаков (как тот же рост и вес пациента), если мы переставим случайно значения одного признака, то у модели останется возможность извлекать информацию об "испорченном" признаке из оставшихся связанных признаков. Это приведёт к занижению важности каждого признака в группе зависимых признаков.

Поэтому рекомендуется вначале разбивать признаки на группы связанных друг с другом признаков, а потом переставлять элементы сразу для всех признаков группы. Так мы оценим важность каждой зависимой группы признаков как целого без смещений.

Также с перестановочной важностью признаков можно ознакомиться в [4]. А в [7] представлен обзор и сравнение различных методов оценки важности признаков.

Перестановочная важность признаков​

Достоинства​

Недостатки​

Литература​

Перестановочная важность признаков

Достоинства

Недостатки

Литература