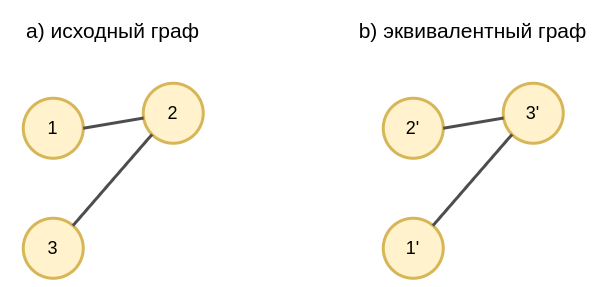
Изоморфизм графов

Вершины графа можно нумеровать произвольным образом, и это не должно оказывать влияния на результат обработки графа. Графы, идентичные друг другу с точностью до перенумерации вершин, называются изоморфными.

Рассмотрим для простоты ненаправленный граф.

Ниже приведён пример исходного графа и его эквивалентной версии, используя следующую перенумерацию вершин:

$$1\to 2',\quad 2\to 3', \quad 3 \to 1'$$

В общем случае для графа, состоящего из $N$ вершин, существует $N(N-1)\cdot...\cdot 1=N!$ перенумераций его вершин.

Матрица перестановок

Перенумерацию вершин можно задать матрицей перестановок (permutation matrix) $P\in\mathbb{R}^{N\times N}$, формируемой по правилу:

$$p_{ij}= \begin{cases} 1, & \text{если $i$-й узел перенумеруется $j$-м узлом,} \\ 0, & \text{иначе.} \end{cases}$$

Перестановочная матрица для перенумерации выше будет:

$$P=\left(\begin{array}{ccc} 0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0 \end{array}\right)$$

Заметим, что

$$P\cdot P^T=P^T\cdot P=I \quad \text{(единичная матрица)},$$

поскольку

$$\{P\cdot P^T\}_{ij} = \sum_{k=1}^N p_{ik}p_{jk}= \begin{cases} 1, & i=j, \\ 0, & i\ne j. \end{cases}$$

Следовательно $P^T$ соответствует обратной перенумерации к $P$.

Преобразование матрицы данных

Рассмотрим, как при изоморфизме можно преобразовывать матрицу данных, содержащую по столбцам данные, ассоциированные с каждой вершиной графа.

Рассмотрим изоморфные графы:

Пусть в исходном графе узлам были сопоставлены данные:

$$v_{1}\to\left(\begin{array}{c} 1\\ 2\\ 3\\ 4 \end{array}\right),\quad v_{2}\to\left(\begin{array}{c} 10\\ 20\\ 30\\ 40 \end{array}\right),\quad v_{3}\to\left(\begin{array}{c} 100\\ 200\\ 300\\ 400 \end{array}\right)$$

а исходная матрица данных имела вид:

$$H=\left(\begin{array}{ccc} 1 & 10 & 100\\ 2 & 20 & 200\\ 3 & 30 & 300\\ 4 & 40 & 400 \end{array}\right).$$

После перенумерации соответствующую матрицу данных $X'$ можно получить по правилу:

$$H' = H\cdot P=\left(\begin{array}{ccc} 1 & 10 & 100\\ 2 & 20 & 200\\ 3 & 30 & 300\\ 4 & 40 & 400 \end{array}\right)\cdot\left(\begin{array}{ccc} 0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0 \end{array}\right)=\left(\begin{array}{ccc} 100 & 1 & 10\\ 200 & 2 & 20\\ 300 & 3 & 30\\ 400 & 4 & 40 \end{array}\right)$$

Преобразование матрицы смежности

Рассмотрим, как преобразуется матрица смежности для следующих изоморфных графов:

Матрица смежности исходного графа была:

$$A=\left(\begin{array}{ccc} 0 & 1 & 0\\ 1 & 0 & 1\\ 0 & 1 & 0 \end{array}\right)$$

После перенумерации узлов соответствующую матрицу смежности можно получить по правилу:

$$\begin{aligned} A'=&P^T\cdot A\cdot P \\=& \left(\begin{array}{ccc} 0 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0 \end{array}\right)\cdot\left(\begin{array}{ccc} 0 & 1 & 0\\ 1 & 0 & 1\\ 0 & 1 & 0 \end{array}\right)\cdot\left(\begin{array}{ccc} 0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0 \end{array}\right) \\ =&\left(\begin{array}{ccc} 0 & 0 & 1\\ 0 & 0 & 1\\ 1 & 1 & 0 \end{array}\right), \end{aligned}$$

откуда видно, что первая и вторая вершины должны быть соединены с третьей.

Применённое правило следует из того, что для получения исходной матрицы смежности $A$ по преобразованной $A'$ нужно:

1. перейти от исходной к преобразованной нумерации;

2. найти связи в преобразованной нумерации;

3. отобразить эти связи в терминах исходной нумерации.

Обратное преобразование будет иметь следующий вид:

$$A=P A' P^T$$

Преобразование матрицы степеней

Рассмотрим, как преобразуется матрица степеней для следующих изоморфных графов:

Матрица степеней исходного графа была:

$$D=\left(\begin{array}{ccc} 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 1 \end{array}\right)$$

Матрицу степеней после перенумерации можно получить по правилу

$$\begin{aligned} D'=&P^T\cdot D\cdot P \\=& \left(\begin{array}{ccc} 0 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0 \end{array}\right)\cdot\left(\begin{array}{ccc} 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 1 \end{array}\right)\cdot\left(\begin{array}{ccc} 0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0 \end{array}\right) \\ =&\left(\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 2 \end{array}\right) \end{aligned}$$

Аналогичное правило действует и для обратной матрицы $D^{-1}$.

Литература

1. Граф (wikipedia).
2. Prince S. J. D. Understanding deep learning. – MIT press, 2023.