Cвёрточные графовые сети

Cвёрточные графовые сети (graph convolutional networks) реализуют пересчёт исходных признаковых описаний $\mathbf{x}_i$ соответствующих вершин $v_i$, учитывая контекст, то есть признаковые описания соседних вершин. Пересчёт производится много раз, начиная с $\mathbf{h}^0_i=\mathbf{x}_i$ и получая $\mathbf{h}^1_i,\mathbf{h}^2_i,...\mathbf{h}^K_i$ для каждой вершины $v_i$.

Рассмотрим свёртку, действующую на однослойном (чёрно-белом) изображении:

$$z_{i}^{k+1}=f\left(\sum_{j\in\text{patch}(i)}w_{j}z_{j}^{k}+b\right)\!,$$

где $b$ - смещение, а $\{w_j\}_j$ - веса для соседних пикселей.

Специфика свёртки на графах:

• используется информация только с непосредственных соседних вершин;

• нет понятий верхнего, нижнего, правого и левого соседей.

  Граф может быть повёрнут, но это будет тот же самый граф!

Пересчёт старых эмбеддингов вершин графа $\mathbf{h}^k_m$ в новые $\mathbf{h}^{k+1}_m$ производится по формулам:

$$\begin{aligned}\mathbf{z}_{n}^{k} & =\text{Aggregate}\left(\left\{ \mathbf{h}_{m}^{k}\right\} _{m\in\mathcal{N}(n)}\right)\!, \\ \mathbf{h}_{n}^{k+1} & =\text{Update}\left(\mathbf{h}_{n}^{k}, \mathbf{z}_{n}^{l}\right)\!, \end{aligned}$$

где

• $\text{Aggregate}\left(\cdot\right)$ - функция, агрегирующая информацию с соседних вершин;

• $\text{Update}\left(\cdot\right)$ - функция, обновляющая информацию о текущей вершине, используя её информацию с предыдущей итерации и агрегированную информацию о её соседях.

Функция $\text{Aggregate}\left(\cdot\right)$ должна быть определена для любого числа соседей и не должна зависеть от порядка их обхода, чтобы обеспечить свойство инвариантности к перенумерации вершин. Применение операций Aggregate, а затем Update представляет собой одну итерацию алгоритма обмена сообщениями (message passing neural network [1]), который использует несколько итераций, а начальные значения для вершин определяются их начальными эмбеддингами: $\mathbf{h}^0_n = \mathbf{x}_n, n=1,2,...N.$ Если $\mathbf{x}_n$ не заданы, то их можно инициализировать one-hot закодированным значением числа соседей узла или геометрическими характеристиками вершин (число соседей 1-го, 2-го порядка, меры центральности вершин на графе и т. д.)

Алгоритм передачи сообщений представлен ниже:

ВХОД:

• ненаправленный граф $G=(V,E)$

• начальные эмбеддинги вершин $\{\mathbf{h}^0_n\}$

• функции $\text{Aggregate}\left(\cdot\right)$ и $\text{Update}\left(\cdot\right)$

АЛГОРИТМ:

для $k=1,2,...K$:

• $\mathbf{z}_{n}^{k} =\text{Aggregate}\left(\left\{ \mathbf{h}_{m}^{k}\right\} _{m\in\mathcal{N}(n)}\right)$

• $\mathbf{h}_{n}^{k+1} =\text{Update}\left(\mathbf{h}_{n}^{k}, \mathbf{z}_{n}^{k}\right)$

ВЫХОД:

• итоговые эмбеддинги вершин $\mathbf{h}^K_n,\; n=1,2,...N$

Применение $K$ итераций алгоритма обмена сообщениями аналогично применению $K$ свёрточных слоёв при обработке изображений. Функции Aggregate и Update имеют свои настраиваемые параметры, причём в общем случае они свои на каждой итерации алгоритма.

Каждая итерация алгоритма передачи сообщений - это слой глубокой графовой сети.

Обратим внимание, что каждая итерация алгоритма повышает область видимости (receptive field) результирующего эмбеддинга на один переход по графу аналогично тому, как его повышает последовательное применение свёрток. Это проиллюстрировано ниже для отдельной вершины.

Нулевая итерация (начальный эмбеддинг):

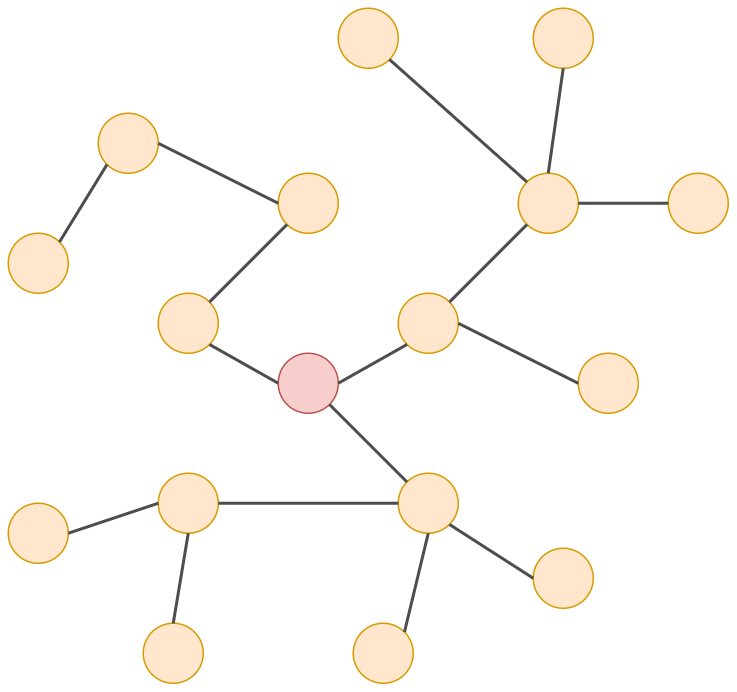
Первая итерация:

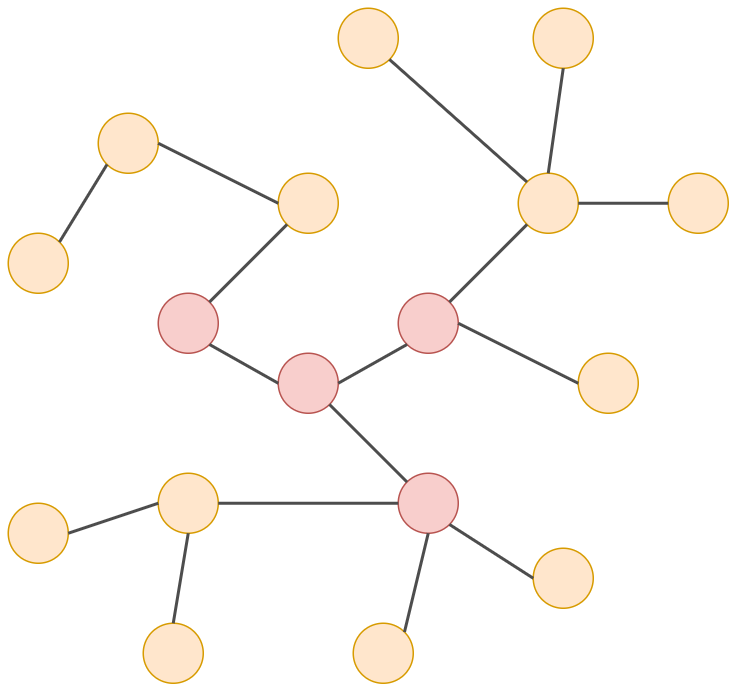
Вторая итерация:

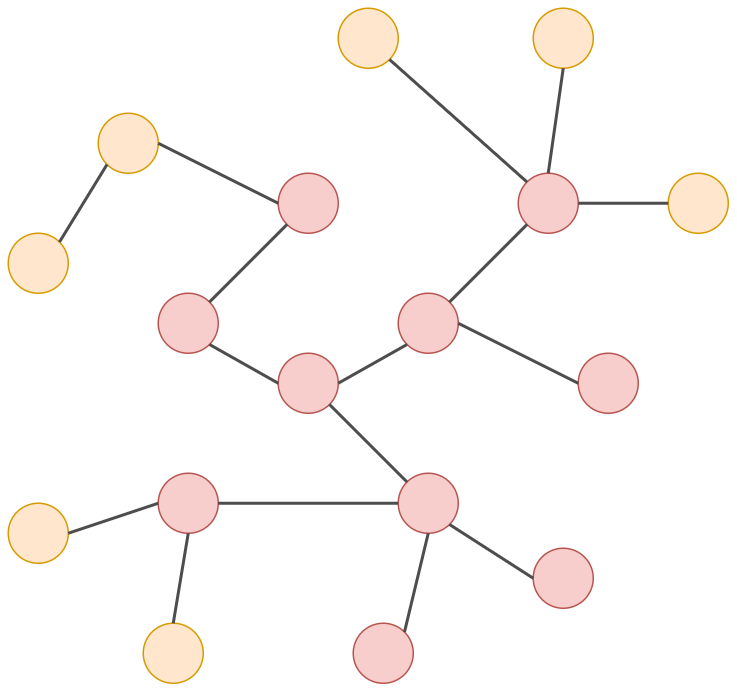
Третья итерация:

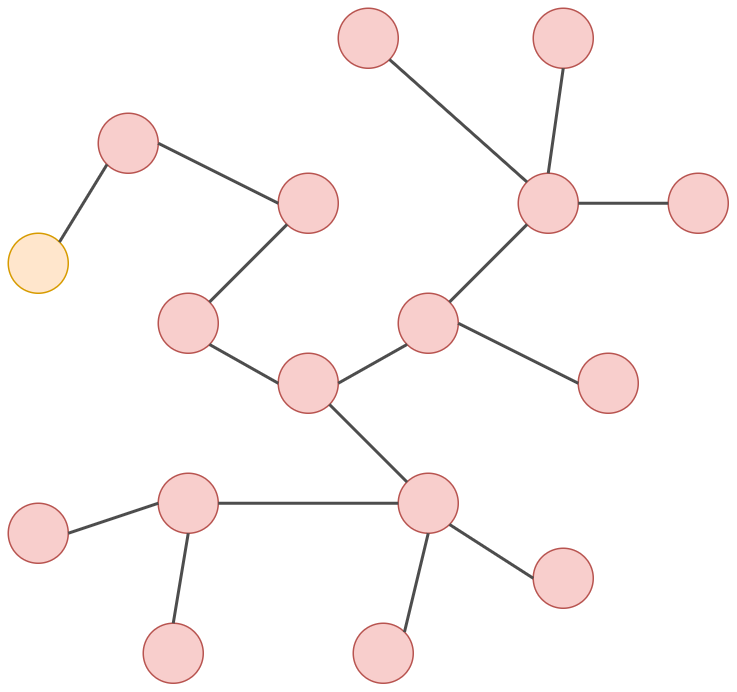
Если граф имеет недостаточную связность, то сообщения между вершинами распространяются медленно. В этом случае связность можно искусственно повысить, добавив в граф дополнительную вершину, связанную со всеми остальными (super-node).

Агрегирующая функция

Функцию Aggregate можно определять по-разному, лишь бы она была определена для любого числа соседей и не зависела от порядка их обхода. Самый простой вариант - сумма эмбеддингов:

$$\text{Aggregate}\left(\cdot\right)=\sum_{m\in\mathcal{N}(n)}\mathbf{h}_{m}^{k},$$

где $\mathcal{N}(n)$ - множество индексов вершин, соединённых ребром с вершиной $n$.

Также можно использовать усреднение:

$$\text{Aggregate}\left(\cdot\right)=\frac{1}{\left|\mathcal{N}(n)\right|}\sum_{m\in\mathcal{N}(n)}\mathbf{h}_{m}^{k}$$

Усреднение по сравнению с суммой работает более устойчиво на вершинах, содержащих сильно различающееся число соседей. Но оно, в отличие от суммы, не способно учитывать зависимость от числа соседей, поскольку при усреднении эта информация теряется.

Также можно усреднять, учитывая различия в числе соседних узлов у каждого соседа [2]:

$$\text{Aggregate}\left(\cdot\right) = \sum_{m\in\mathcal{N}(n)}\frac{1}{\sqrt{\left|\mathcal{N}(n)\right|\cdot\left|\mathcal{N}(m)\right|}}\,\mathbf{h}_{m}^{k}$$

Эмпирически при многократной агрегации на последних слоях алгоритма обмена сообщениями эмбеддинги получаются слишком сглаженными (over-smoothed) за счёт многократных усреднений. Предотвратить этот эффект можно, используя в качестве агрегации поэлементный максимум:

$$\text{Aggregate}\left(\cdot\right)=\text{maximum}\left(\left\{ \mathbf{h}_{m}^{k}\right\} _{m\in\mathcal{N}(n)}\right)$$

Наиболее общим видом усреднения, способным моделировать любую дифференцируемую зависимость, инвариантную к перенумерации вершин, является использование двух многослойных персептронов (multi-layer perceptron, MLP) со своими настраиваемыми векторами параметров $\mathbf{w}$ и $\mathbf{v}$ [3]:

$$\text{Aggregate}\left(\cdot\right)=\text{MLP}_{\mathbf{w}}\left(\sum_{m\in\mathcal{N}(n)}\text{MLP}_{\mathbf{v}}\left(\mathbf{h}_{m}^{k}\right)\right)$$

В последней формуле вместо суммы можно использовать и другие перечисленные выше виды агрегации.

Агрегация со вниманием

Можно использовать механизм внимания (attention mechanism) при агрегации узлов [4] аналогично тому, как он использовался в рекуррентных сетях.

Для этого нужно произвести следующие действия:

1. Вычисляется внимание, с которым узел $v_n$ должен смотреть на каждого своего соседа $v_m$, используя некоторую функцию $g(\cdot)$:

   $$s_{nm}=g(\mathbf{h}^k_n,\mathbf{h}^k_m)$$

2. Коэффициенты внимания пропускаются через SoftMax-преобразование:

   $$\left\{ a_{nm}\right\}_{m\in\mathcal{N}(n)}=\text{SoftMax}\left(\left\{ s_{nm}\right\}_{m\in\mathcal{N}(n)}\right)$$

3. Агрегация информации с узлов осуществляется пропорционально найденному вниманию:

   $$\mathbf{z}_{n}^{k}=\sum_{n\in\mathcal{N}(n)}a_{nm}\mathbf{h}_{m}^{k}$$

Например, внимание может вычисляться через билинейную форму с настраиваемой матрицей $W\in\mathbb{R}^{D\times D}$:

$$a_{mn}=\frac{\text{exp}\left(\mathbf{h}_{n}^{T}W\mathbf{h}_{m}\right)}{\sum_{m'\in\mathcal{N}(n)}\text{exp}\left(\mathbf{h}_{n}^{T}W\mathbf{h}_{m'}\right)}$$

В более общем случае внимание может вычисляться через многослойный персептрон:

$$a_{mn}=\frac{\text{exp}\left(\text{MLP}\left(\mathbf{h}_{n},\mathbf{h}_{m}\right)\right)}{\sum_{m'\in\mathcal{N}(n)}\text{exp}\left(\text{MLP}\left(\mathbf{h}_{n},\mathbf{h}_{m'}\right)\right)}$$

Графовые сети с механизмом внимания называются graph attention networks (GAT).

Аналогично тому, как это сделано в трансформере, можно применять несколько головок внимания со своими весами, конкатенировать полученные результаты и приводить результат к исходному $D$-мерному пространству эмбеддингов, используя линейный слой.

Обновляющая функция

Типичным способом определения функции Update является использование одного линейного слоя:

$$\mathbf{h}^{k+1}_n=\text{Update}\left(\mathbf{h}_{n}^{k},\mathbf{z}_{n}^{k}\right)=f\left(W\mathbf{h}^{k}+V\mathbf{z}_{n}^{k}+\mathbf{b}\right)\!,$$

где $f(\cdot)$ - функция активации, применяемая поэлементно. Популярный способ передачи сообщений - агрегировать суммированием и использовать одну и ту же матрицу весов для целевого узла и его соседей:

$$\mathbf{h}_{n}^{k+1}=f\left(W\!\!\!\!\sum_{m\in\mathcal{N}(n)\cup n}\mathbf{h}_{m}^{k}+\mathbf{b}\right)$$

Чтобы облегчить настройку параметров сети, а также частично избавиться от сглаживания эмбеддингов (когда они становятся слишком похожими за счёт повторного усреднения по ним) можно использовать в качестве выхода сумму преобразования с исходным входом (остаточный блок), как было в модели ResNet:

$$\mathbf{h}_{n}^{k+1}=\text{Update}\left(\mathbf{h}_{n}^{k},\mathbf{z}_{n}^{k}\right)+\mathbf{h}_{n}^{k}$$

Альтернативно в качестве итогового представления каждой вершины можно использовать конкатенацию её представлений на всех итерациях передачи сообщений:

$$\mathbf{h}^{\text{final}}_n = [\mathbf{h}^1_n; \mathbf{h}^1_n; ... \mathbf{h}^K_n]$$

Тогда даже при сглаживании на последних итерациях эмбеддинги вершин всё равно будут существенно различаться за счёт учёта эмбеддингов с более ранних итераций.

С учётом признаков с разных слоёв сети мы уже сталкивались в модели DenseNet.

Инвариантность к перенумерациям

В матричном виде операции Aggregate и Update можно описать цепочкой преобразований

$$\begin{aligned}H^{1} & =F\left(X,A,W^{1}\right)\!; \\ H^{2} & =F\left(H^{1},A,W^{2}\right)\!; \\ & \cdots \\ H^{K} & =F\left(H^{K-1},A,W^{K}\right)\!; \end{aligned}$$

где

• $A$ - матрица смежности вершин,

• $H^i=[\mathbf{h}^i_1,...\mathbf{h}^i_N]\in\mathbb{R}^{D\times N}$ - матрица, столбцы которой являются внутренними представлениями узлов на $i$-м шаге алгоритма обмена сообщениями;

• $X\in\mathbb{R}^{D\times N}$ - матрица начальных эмбеддингов вершин;

• $W^i$ - матрица настраиваемых весов на $i$-м шаге.

На каждом шаге алгоритма передачи сообщений преобразование $F(\cdot)$ должно обладать эквивариантностью к перенумерации узлов (equivariance) - если вершины перенумеровать, то и результат их обработки должен перенумероваться соответствующим образом.

$$H^{k}P = F\left(H^{k}P,\;P^T\cdot A\cdot P,\;W^{k}\right)$$

Задача

Запишите в матричном виде описанные выше операции Aggregate и Update. Для операций усреднения вам понадобится матрица степеней. Для каждой записи в матричном виде докажите, что для неё выполнено свойство эквивариантности. Для этого вам пригодятся формулы пересчёта матрицы данных, матрицы смежности и матрицы, обратной к матрице степеней при перенумерации вершин графа.

Учёт эмбеддингов рёбер и всего графа

Алгоритм передачи сообщений в графе можно обобщить, чтобы он обновлял и учитывал в обновлении не только эмбеддинги вершин $\mathbf{h}_{n}^{k}$, но также эмбеддинги рёбер $\mathbf{e}_{nm}^{k}$ и всего графа целиком $\mathbf{g}^{k}$ (general message passing [5]).

Обобщённый алгоритм передачи сообщений:

ВХОД:

• ненаправленный граф $G=(V,E)$

• начальные эмбеддинги вершин $\{\mathbf{h}^0_n\}$

• начальные эмбеддинги рёбер $\{\mathbf{e}^0_{nm}\}$

• начальный эмбеддинг графа $\mathbf{g}^0$

• функции $\text{Aggregate}\left(\cdot\right)$ и $\text{Update}\left(\cdot\right)$

АЛГОРИТМ:

для $k=1,2,...K$:

• $\mathbf{e}_{nm}^{k+1}=\text{Update}_{\text{edge}}\left(\mathbf{e}_{nm}^{k},\mathbf{h}_{n}^{k},\mathbf{h}_{m}^{k},\mathbf{g}^{k}\right)$

• $\mathbf{z}_{n}^{k+1}=\text{Aggregate}_{\text{node}}\left(\left\{ \mathbf{e}_{nm}^{k+1}\right\} _{m\in\mathcal{N}(n)}\right)$

• $\mathbf{h}_{n}^{k+1}=\text{Update}_{\text{node}}\left(\mathbf{h}_{n}^{k+1},\mathbf{z}_{n}^{k+1},\mathbf{g}^{k}\right)$

• $\mathbf{g}_{n}^{k+1}=\text{Update}_\text{graph}\left(\mathbf{g}^{k},\text{GlobalAggregate}_{\text{node}} \left( \left\{ \mathbf{h}_{n}^{k+1}\right\}\right) ,\text{GlobalAggregate}_{\text{edge}} \left(\left\{ \mathbf{e}_{nm}^{k+1}\right\}\right) \right)$

ВЫХОД:

• итоговые эмбеддинги $\left\{ \mathbf{h}_{n}^{K}\right\} ,\left\{ \mathbf{e}_{nm}^{K}\right\} ,\mathbf{g}^{K}$

Как видим, алгоритм состоит из следующих шагов:

1. обновляются эмбеддинги каждого ребра по его старому эмбеддингу, эмбеддингам вершин ребра и графа целиком;

2. обновляется эмбеддинг контекста каждой вершины по эмбеддингам связанных с ним рёбер;

3. происходит обновление эмбеддинга вершины по её старому эмбеддингу, контексту и эмбеддингу всего графа;

4. обновляется эмбеддинг всего графа, используя его старый эмбеддинг и агрегацию по обновлённым эмбеддингам вершин и рёбер.

Учёт взаимных влияний признаков вершин, рёбер и графа целиком позволяет моделировать сложные взаимодействия, решая весь комплекс задач на графах:

• предсказание свойств узлов;

• предсказание свойств рёбер;

• предсказание свойств графа целиком.

---

Далее мы рассмотрим особенности обучения графовых сетей и изучим геометрические способы извлечения эмбеддингов вершин графа, не использующие никаких внешних признаков вершин, а учитывающие только их геометрическое расположение на графе.

Литература

1. Gilmer J. et al. Neural message passing for quantum chemistry //International conference on machine learning. – PMLR, 2017. – С. 1263-1272.
2. Kipf T. N., Welling M. Semi-supervised classification with graph convolutional networks //arXiv preprint arXiv:1609.02907. – 2016.
3. Zaheer M. et al. Deep sets //Advances in neural information processing systems. – 2017. – Т. 30.
4. Veličković P. et al. Graph attention networks //arXiv preprint arXiv:1710.10903. – 2017.
5. Battaglia P. W. et al. Relational inductive biases, deep learning, and graph networks //arXiv preprint arXiv:1806.01261. – 2018.