Перейти к основному содержимому

Альтернативные эмбеддинги вершин

Алгоритм передачи сообщений в свёрточных графовых сетях - это основной метод уточнения уже имеющихся признаковых описаний вершин графа по их соседям.

В этой главе мы изучим способы построения эмбеддингов вершин графа, которые не предполагают начальных признаковых описаний вершин, а строятся с учётом только геометрии самого графа. Результирующие эмбеддинги в итоге лучше отражают структуру графа.

Задачей, рассматриваемой в этой главе, будет построение DD-мерных эмбеддингов для одного большого графа, состоящего из NN вершин. В дальнейшем полученные эмбеддинги могут использоваться для решения любой задачи на графах.

Эмбеддинги на основе случайных блужданий​

Рассмотрим методы построения эмбеддингов, основанные на случайном блуждании по графу (random walk), при котором генерируются пути обхода графа, стартуя из случайных вершин и перемещаясь по нему, выбирая случайных соседей. Начальные эмбеддинги инициализируются случайно либо на основе характеристик, известных для каждой вершины графа. В процессе генерации путей обхода сближаются эмбеддинги вершин, оказавшихся недалеко друг от друга.

DeepWalk​

В методе DeepWalk [1] из каждой вершины KK раз запускается процесс случайного блуждания длины MM. Если трактовать каждую вершину как слово, то в результате получается K⋅NK\cdot N предложений длины MM каждое.

Для уточнения эмбеддингов по их расположениям на графе в DeepWalk предлагается использовать метод SkipGram модели Word2Vec, в котором по каждому сгенерированному пути на графе скользит окно ширины 2W+12W+1, и настраивается модель, пытающаяся по эмбеддингу центральной вершины окна предсказать другие вершины в том же окне аналогично тому, как в оригинальной модели SkipGram строилась языковая модель, предсказывавшая соседние слова окна по центральному слову. Параметрами настроенной модели и будут эмбеддинги вершин графа с учётом его геометрии, поскольку близким вершинам будут соответствовать более близкие эмбеддинги (с более высоким попарным скалярным произведением).

Идеи расширения метода

Обратим внимание, что, используя ту же методологию, можно строить эмбеддинги вершин графа, используя C-BOW версию модели Word2Vec или другую языковую модель, подбирающую эмбеддинги под слова.

Сравнение DeepWalk и алгоритма передачи сообщений

Метод DeepWalk более экономичен по памяти, чем алгоритм передачи сообщений (message passing algorithm) в классических графовых нейросетях, поскольку передача сообщений требует аккумуляции информации со всех соседей каждой вершины, в то время как настройка DeepWalk предполагает переходы лишь по одной случайно выбираемой каждый раз вершине.

С другой стороны, выбирая каждый раз лишь одну из соседних вершин, методу DeepWalk потребуется больше итераций до сходимости, поскольку лишь многократные обходы вершин смогут собрать информацию о большинстве соседей.

Node2Vec​

Модель Node2Vec [2] также уточняет эмбеддинги вершин графа, учитывая его геометрию. Она использует тот же механизм построения эмбеддингов, что и DeepWalk:

  • каждому узлу графа сопоставляется начальный эмбеддинг (случайно или используя известные характеристики);

  • из каждого узла генерируются случайные блуждания (random walks) по соседним узлам;

  • в сгенерированных блужданиях перебираются всевозможные последовательности узлов фиксированной длины (окна наблюдений);

  • в каждом окне наблюдений модель по эмбеддингу центральной вершины в окне настраивается предсказывать другие вершины в том же окне.

Ключевой идеей Node2Vec является наблюдение, что обход вершин графа из заданной вершины может быть устроен по-разному:

  • поиск в ширину (breadth-first search, BFS), при котором обход осуществляется в первую очередь по вершинам в окрестности начальной вершины;

  • поиск в глубину (depth-first search, DFS), при котором обход осуществляется таким образом, чтобы уходить максимально далеко от первоначальной вершины.

Эти две стратегии проиллюстрированы ниже красным и синим цветом [2]:

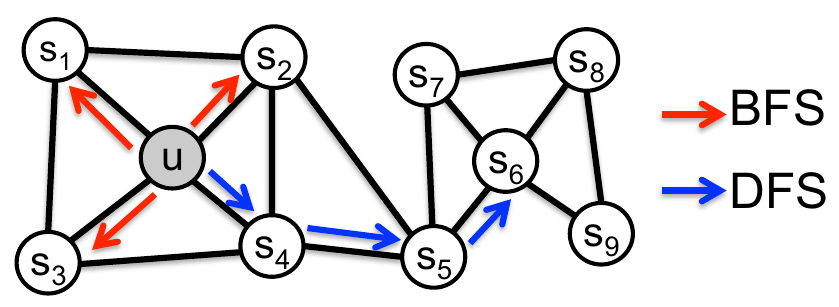
Метод Node2Vec использует случайное блуждание 2-го порядка (2-nd order random walk) с гиперпараметрами p,q>0p,q>0, управляющими характером обхода вершин, больше склоняющимся к обходу в глубину или обходу в ширину.

В частности, если только осуществился переход из вершины tt в вершину vv, то вероятность перехода из вершины vv в новую вершину xx считается по формуле:

p(v→x∣v,t)={γ⋅1pесли x=t,γ⋅1если d(t,x)=1,γ⋅1qесли d(t,x)=2,p(v\to x|v,t)=\begin{cases} \gamma \cdot \frac{1}{p} & \text{если }x=t,\\ \gamma \cdot 1 & \text{если }d\left(t,x\right)=1,\\ \gamma \cdot \frac{1}{q} & \text{если }d\left(t,x\right)=2, \end{cases}

где d(t,x)d(t,x) - длина минимального пути от вершины tt в вершину xx, а γ\gamma - нормировочный множитель, чтобы все вероятности суммировались в единицу.

Пример ненормированных вероятностей перехода из вершины vv приведён ниже [2]:

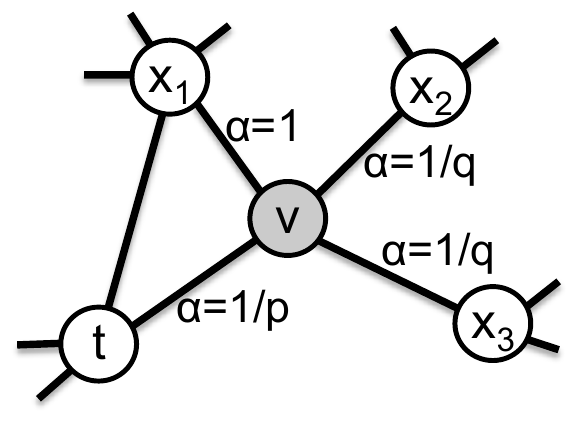
Если рёбра на графе являются взвешенными (ребрам сопоставлены числа, обозначающие силу связи), то вероятности переходов нужно ещё дополнительно домножать на веса соответствующих связей.

Как гиперпараметры p,qp,q влияют на характер обхода графа (в глубину/в ширину)?

При малых значениях pp обход будет вестись скорее в ширину, поскольку будут частые возвращения в исходную вершину. Малые значения qq, наоборот, стимулируют поиск в глубину.

Обход в глубину выделяет сообщества в графе (подмножества сильно связанных друг с другом вершин напрямую или опосредованно) - у таких узлов будут схожие эмбеддинги.

Обход в ширину определяет структурные роли вершин (structural roles of nodes), т.е. является ли вершина:

  • хабом (центральным узлом в сообществе, имеющим короткие пути до остальных вершин сообщества);

  • связующим узлом (связывает несколько сообществ между собой);

  • периферийной вершиной (находящейся на краю графа).

Рассмотрим граф, состоящий из персонажей романа Виктора Гюго "Отверженные". Узлы соединяются ребром, если персонажи взаимодействовали друг с другом в тексте. Если эмбеддинги вершин извлекать методом Node2Vec, а потом кластеризовать и кластер обозначать цветом, то получим результат ниже, где сверху осуществлялся обход в глубину (и были выделены сообщества персонажей), а снизу - обход в ширину (и были выделены структурные роли каждого персонажа) [2]:

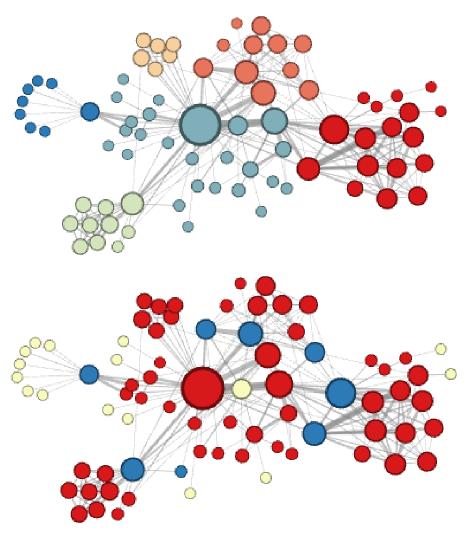
Использование автокодировщика​

Каждую вершину графа можно охарактеризовать тем, с какими другими вершинами она связана, аналогично тому, как слова в тексте по смыслу характеризуются тем, с какими словами они совстречались вместе.

Поэтому вершину можно характеризовать соответствующей строкой (или столбцом) в матрице смежности (adjency matrix). Но это слишком длинный эмбеддинг, совпадающий по размерности с числом вершин всего графа. К тому же он учитывает только соседей первого порядка.

Для более общих и компактных эмбеддингов к строкам матрицы смежности можно применить методы снижения размерности, в частности, извлекать их как внутреннее представление в середине автокодировщика, через который пропущена соответствующая строка. Сам автокодировщик при этом обучен восстанавливать строки матрицы смежности целиком.

Переобучение

Поскольку обучающими примерами для автокодировщика будут строки матрицы смежности, то число обучающих примеров совпадёт с числом вершин в графе NN. Но число параметров автокодировщика также растёт линейно с увеличением размерности входа и будет больше NN. Поэтому при использовании такого подхода нужно уделить повышенное внимание регуляризации, чтобы модель не переобучалась!

Предложенный подход используется, например, в статье [3], в которой предложены способы регуляризации для борьбы с переобучением. Архитектура позволяет выдавать эмбеддинг для новых вершин за один проход по автокодировщику, правда, после появления новых вершин сам автокодировщик нужно донастраивать.

Совмещение подходов​

Представленные подходы выделяют эмбеддинги, направленные на описание геометрии графа, и они хорошо справляются с этой задачей. Свёрточные графовые нейросети (GCN) призваны уточнять признаковые описания вершин по их соседям. Эти подходы можно объединить одним из двух способов:

  • Использовать геометрические эмбеддинги как инициализацию признаковых описаний вершин для GCN (если другие характеристики вершин неизвестны);

  • Дополнить начальные признаковые описания вершин их геометрическими эмбеддингами перед применением GCN (если есть дополнительная информация о вершинах).

Литература​

  1. Perozzi B., Al-Rfou R., Skiena S. Deepwalk: Online learning of social representations //Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. – 2014. – С. 701-710.
  2. Grover A., Leskovec J. node2vec: Scalable feature learning for networks //Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining. – 2016. – С. 855-864.
  3. Wang D., Cui P., Zhu W. Structural deep network embedding //Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining. – 2016. – С. 1225-1234.