Типы графов

Граф (graph) [1] представляет собой структуру данных, состоящую из узлов (называемых также вершинами графа, nodes, vertices) $V=\{v_1,v_2,...v_N\}$, некоторые из которых соединены рёбрами (связями, edges) $E=\{(v_i,v_j)\}_{i,j\text{ соединены}}$.

Рассмотрим основные виды графов и их обобщения, а также описание геометрии графов в виде матриц смежности и матриц степеней.

Ненаправленный граф

В ненаправленном графе (или неориентированном, undirected graph) рёбра не имеют направления: если вершина $v_i$ соединена с $v_j$, то $v_j$ симметрично соединена с $v_i$.

Пример ненаправленного графа:

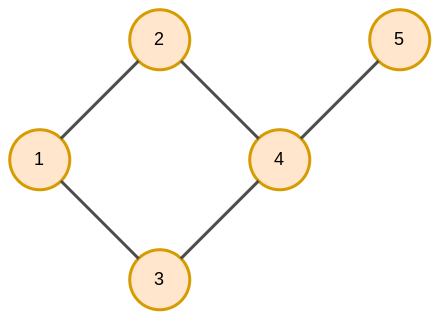
В нём 5 вершин и 5 ребер $(v_1,v_2),(v_2,v_4),(v_4,v_3),(v_4,v_1)$ и $(v_4,v_5)$.

Примеры данных, описываемых ненаправленным графом:

• молекула, в которой узлами являются атомы, а рёбрами - химические связи;

• электрические схемы, в которых узлами являются элементы схемы, а рёбрами - провода между ними;

• социальная сеть, где узлами выступают пользователи, а рёбрами - отношения взаимной дружбы между ними;

• туристическая карта, в которой узлами выступают локации, а рёбрами - пешеходные дороги между ними.

Направленный граф

В направленном графе (или ориентированном, directed graph) рёбра имеют направления. Для каждого ребра известно, из какой вершины оно выходит и в какую приходит.

Пример направленного графа приведён ниже:

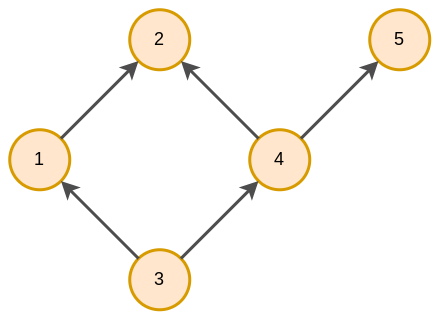
Примеры данных, описываемых направленным графом:

• социальная сеть, где узлами выступают пользователи, а рёбрами - их подписки на новости друг друга;

• система передачи данных, где узлами обозначаются элементы системы, а рёбрами - потоки данных между ними;

• автомобильная дорожная сеть, где узлами являются перекрёстки, а рёбрами - направления движения на дорогах.

Смешанный граф

Смешанный граф (mixed graph) содержит как направленные, так и ненаправленные рёбра.

Примеры данных, описываемых смешанным графом:

• транспортные сети, где узлами выступают перекрёстки, а рёбрами - связи односторонними и двусторонними дорогами;

• энергетические системы, где узлами выступают станции перераспределения, генераторы и потребители, а связями - линии передачи энергии.

Далее, для простоты, будут рассматриваться только ненаправленные графы, хотя приводимые выводы можно обобщить и для направленных и смешанных графов.

Ассоциированные данные

Каждой вершине графа $v_i$ может быть сопоставлен свой $D$-мерный вектор признаков $\mathbf{h}_i$:

$$v_i \to \mathbf{h}_i \in \mathbb{R}^D$$

Например, в социальной сети это могут быть характеристики пользователя.

Аналогично каждому ребру может сопоставляться свой вектор данных:

$$c_j \to \mathbf{e}_j \in \mathbb{R}^{D_e}$$

В графе социальной сети связи могут дополняться информацией, которую пользователи пересылают друг другу.

Также всему графу целиком может сопоставляться вектор данных $\mathbf{g}\in\mathbb{R}^{D_g}$, описывающий весь граф.

Графу, описывающему молекулярное соединение, может сопоставляться информация о физических и химических свойствах этого соединения.

Ниже приведён пример графа с визуализацией векторов данных, описывающих свойства вершин, рёбер и свойств всего графа целиком:

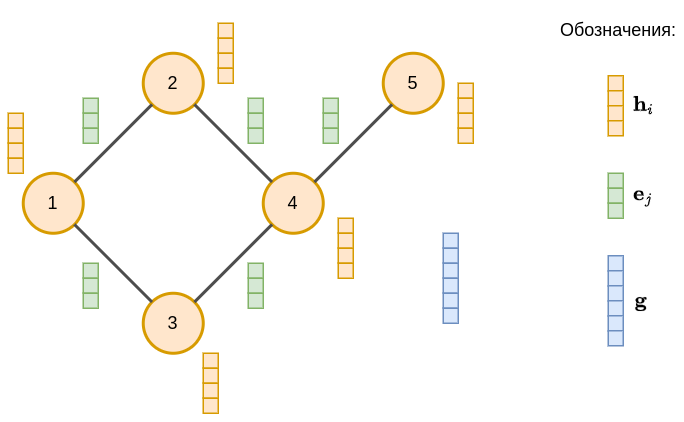
Чаще всего рассматриваются только данные, ассоциированные узлам, которые можно объединить в матрицу $H=[\mathbf{h}_1,...\mathbf{h}_N]\in\mathbb{R}^{D\times N}$, в которой $j$-му столбцу соответствует вектор $\mathbf{h}_j$, описывающий характеристики вершины $v_j$.

Граф рёбер

По исходному графу можно построить сопряжённый граф рёбер (edge graph), в котором

• каждая связь исходного графа становится узлом;

• узлы сопряжённого графа соединяются, если соответствующие им рёбра имеют общий узел в исходном графе.

Пример (a) исходного графа (b) выделения рёбер в узлы и (c) сопряжённого графа рёбер приведён ниже:

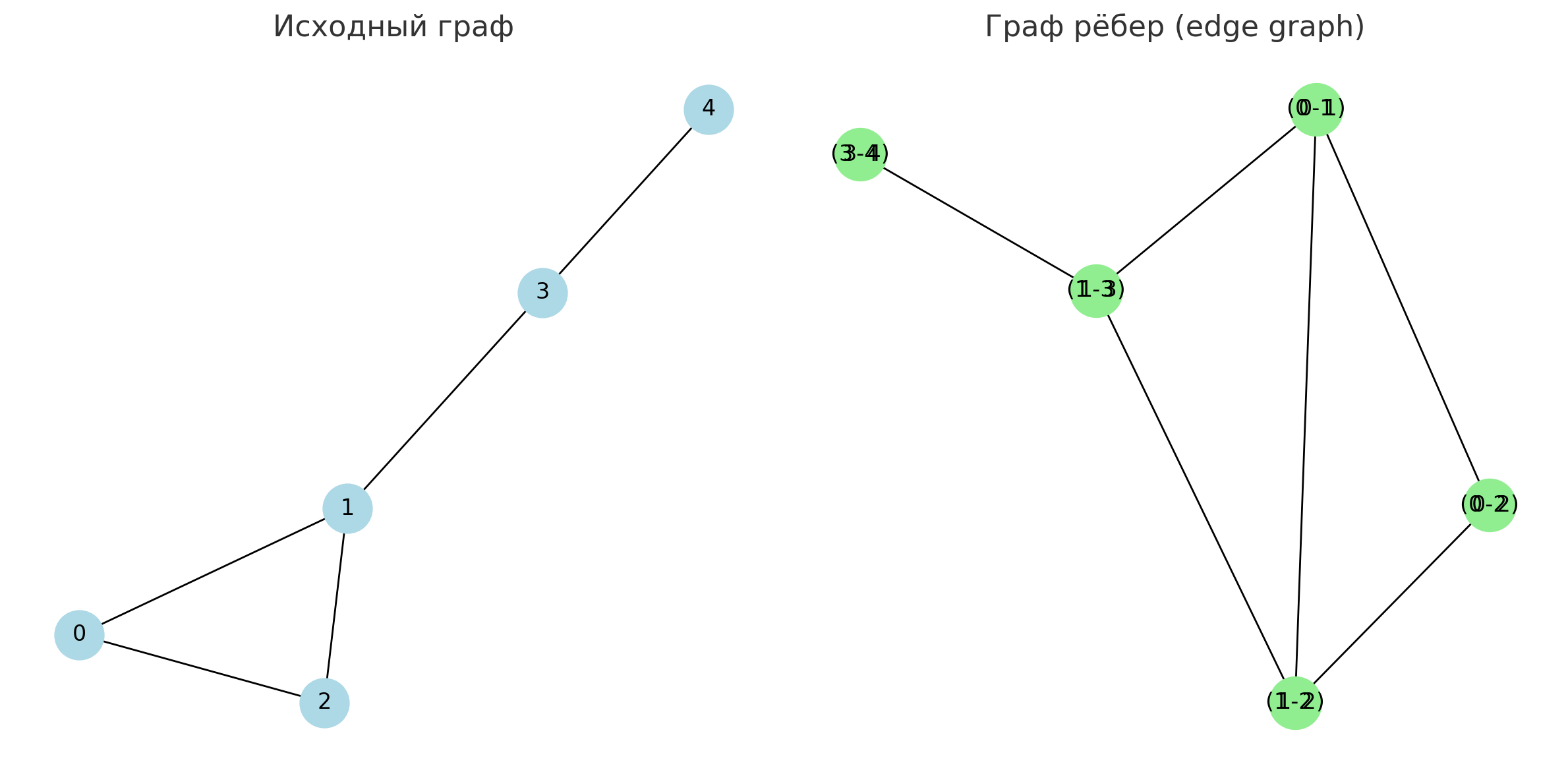
По сопряжённому графу рёбер можно обратно восстановить исходный граф.

Мультиграфы

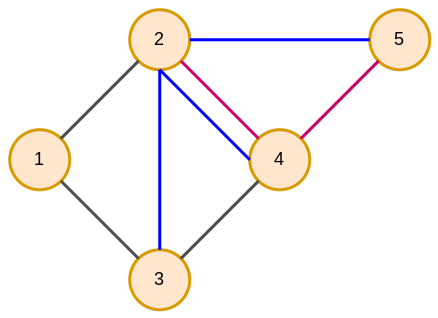
Существуют структуры данных, описываемые мультиграфами (multigraph), в которых узлы могут соединяться рёбрами разных типов, обозначенными в примере ниже цветом:

Примеры данных, описываемых мультиграфом:

• социальная сеть, в которой узлы - пользователи, которые могут вступать в разные виды взаимодействия (ставить лайки, писать комментарии, подписываться друг на друга);

• логистическая сеть, где узлы - локации, по которым можно перемещаться, используя разный вид транспорта (на автобусе, метро или самолёте).

Гетерогенные графы

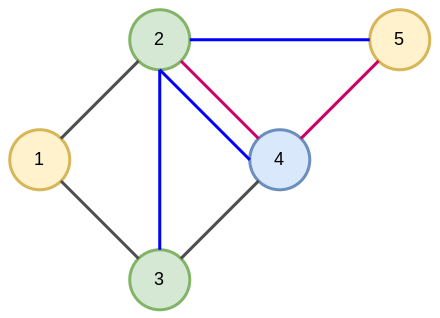
Гетерогенные графы (heterogeneous graph) - это графы, состоящие из узлов разных типов. Ниже приведён пример гетерогенного мультиграфа, на котором узлы и рёбра разных типов обозначены различными цветами:

Примеры данных, описываемых гетерогенным графом:

• торговая система, в которой узлами выступают пользователи, товары и продавцы, взаимодействующие друг с другом;

• граф знаний, в котором узлами являются персоны, компании, страны и события, связанные друг с другом.

Матрица смежности

Рёбра графа из $N$ вершин описываются матрицей смежности (adjency matrix) $A\in\mathbb{R}^{N \times N}$.

Ненаправленный граф

Для ненаправленного графа элементы матрицы смежности формируются по правилу:

$$a_{ij}= \begin{cases} 1, & \text{ если $v_i$ и $v_j$ соединены ребром,} \\ 0, & \text{ иначе.} \end{cases}$$

Рассмотрим граф:

Для него матрица смежности будет

$$A=\left(\begin{array}{ccccc} 0 & 1 & 1 & 0 & 0\\ 1 & 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 1 & 0\\ 0 & 1 & 1 & 0 & 1\\ 0 & 0 & 0 & 1 & 0 \end{array}\right)$$

Эта матрица будет симметричной ($A=A^T$), поскольку если $(v_i,v_j)$ соединены ребром, то в ненаправленном графе ребром также будут соединены и $(v_j,v_i)$.

Направленный граф

Для направленного графа элементы матрицы смежности формируются по правилу:

$$a_{ij}= \begin{cases} 1, & \text{ если ребро выходит из $v_j$ в $v_i$,} \\ 0, & \text{ иначе.} \end{cases}$$

Рассмотрим граф:

Для него матрица смежности будет

$$A=\left(\begin{array}{ccccc} 0 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 \end{array}\right)$$

Для направленного графа матрица смежности уже не обязательно будет симметричной.

Свойство матрицы смежности

Если $\mathbf{o}_i$ - one-hot закодированная вершина $v_i$, то

$$\begin{aligned} A \cdot \mathbf{o}_{i} & \text{ - число путей длины 1 до вершин из }v_{i}\\ A \cdot A\cdot\mathbf{o}_{i} & \text{ - число путей длины 2 до вершин из }v_{i}\\ A \cdot A\cdot A\cdot\mathbf{o}_{i} & \text{ - число путей длины 3 до вершин из }v_{i}\\ \cdots & \cdots \end{aligned}$$

В общем случае, $A^n\cdot\mathbf{o}_{i} \in\mathbb{R}^{N}$ - число путей длины $n$ из вершины $v_i$ до всех других вершин графа. При этом в расчёте числа путей допускается посещение каждой вершины и проход по одному и тому же ребру несколько раз.

Минимальное $n$, при котором $j$-й элемент $\{A^n\cdot\mathbf{o}_{i}\}_j>0$, будет длиной маршрута из $v_i$ в $v_j$.

Матрица степеней

Также для графа рассматривают матрицу степеней (degree matrix) - диагональную матрицу $D\in\mathbb{R}^{N\times N}$, в которой $d_{ii}$ равно числу связей $i$-й вершины с другими вершинами. При этом для направленного графа различают матрицу степеней для входящих и исходящих рёбер.

Рассмотрим граф:

Для него матрица степеней будет

$$D=\left(\begin{array}{ccccc} 2 & 0 & 0 & 0 & 0\\ 0 & 2 & 0 & 0 & 0\\ 0 & 0 & 2 & 0 & 0\\ 0 & 0 & 0 & 3 & 0\\ 0 & 0 & 0 & 0 & 1 \end{array}\right)$$

---

Важно понимать, что вершины в графе можно нумеровать в произвольном порядке: если их перенумеровать, то, по сути, это будет тот же самый граф, и модели, обрабатывающие графы, не должны зависеть от перенумерации вершин. Графы, эквивалентные с точностью до перенумерации вершин, называются изоморфными. Изоморфизму в графах посвящена следующая глава.

Далее мы рассмотрим, какие задачи можно решать на графах, изучим подходы к их решению, используя глубокое обучение, а потом разберём основной использующийся для этого нейросетевой метод - свёрточные графовые сети.

Литература

1. Wikipedia: Граф (математика).