Задачи на графах

Типы задач на графах

Рассмотрим популярные задачи на графах, решаемых нейросетями:

1. Для части узлов графа известно некоторое свойство. Необходимо восстановить это свойство для остальных узлов (node classification/regression).

2. Для части рёбер которого известно некоторое свойство. Необходимо восстановить это свойство для других рёбер (edge classification/regression).

   Отметим, что эта задача сводится к предыдущей, если перейти от исходного графа к графу рёбер (edge graph), заменив связи вершинами, а данные новых узлов задать как данные соответствующих им рёбер первоначального графа.

3. Дан граф, лишь часть рёбер которого известны. Необходимо восстановить недостающие рёбра (link prediction).

4. Дан набор графов, каждый из которых, как целое, обладает некоторым свойством. Необходимо восстановить это свойство для других похожих графов (graph classification/regression).

5. Обнаружение сообществ в графе (community detection) — задача выделения подмножеств узлов, внутри которых связи плотнее, чем с остальными частями графа. Примером сообщества могут быть группы людей с высокой степенью общения — такие как друзья, одноклассники или коллеги. Задача обычно решается вычислительными методами без использования нейросетей.

6. Генерация графов, обладающих требуемыми свойствами (graph generation). Данная задача решается генеративными методами глубокого обучения, такими как генеративно-состязательные сети.

Примеры прикладных задач

Социальная сеть

Социальную сеть (social network) можно рассматривать как граф, в котором узлами являются люди, а связи устанавливаются, если они:

• добавили друг друга в друзья;

• подписаны друг на друга;

• писали друг другу сообщения.

Узлу соответствуют данные, которые пользователь о себе указал (пол, возраст, интересы), а также информация о поведении в сети (сколько раз заходил, просматривал новости, писал сообщения). Рёбрам можно поставить в соответствие интенсивность общения (сколько раз писали друг другу сообщения, заходили на страницы друг друга, ставили реакции на посты).

Примеры задачи для социальной сети:

• предсказание свойства узла:

  • определение тем, которые человеку могли бы быть интересны;

  • оценка возраста (если не указан), материального статуса;

  • предсказание поведения (вероятность клика или покупки);

  • обнаружение аномалий (соответствующих тому, что аккаунт является ботом или мошенником).

• восстановление рёбер:

  • рекомендация друзей, постов, групп.

Граф цитирований

Граф цитирований (citation graph) описывает научные работы, выступающие узлами этого графа. Узел соединяется с другим узлом, если научная работа ссылается на другую. Поскольку цитирование - несимметричная операция, то это всегда будет направленный граф.

Примеры задач, решаемых на графе цитирований:

• предсказание свойств узла:

  • оценка тематики и научной ценности работы по её содержанию и ссылкам на неё из других работ;

• восстановление рёбер:

  • рекомендация новых релевантных ссылок для научной работы, определение связанных друг с другом исследований, даже если они явно не ссылаются друг на друга.

• обнаружение сообществ одноклассников, коллег по работе.

Интернет

Интернет можно описать графом (network graph), в котором узлами являются веб-страницы, а ребро проводится, если одна веб-страница содержит гиперссылку на другую. Как и в случае графа цитирований, это будет направленный граф.

Задачи, которые можно решать:

• предсказание свойства узла:
  • оценка тематики веб-страницы;
  • оценка важности веб-страницы для оценки её позиции в поисковой выдаче;
• восстановление рёбер:
  • определение веб-страниц схожей тематики, даже если они не ссылаются друг на друга.
• обнаружение сообществ, отвечающих различным направлениям научных исследований.

Химические соединения

Вещества можно описать химической формулой, а, следовательно, в виде графа, в котором узлами будут являться атомы, а рёбра будут описывать химические связи между ними.

Химические соединения описываются небольшими графами. Многие соединения уже хорошо исследованы, и их свойства известны. Возникает задача для новых гипотетических соединений предсказать их ожидаемые свойства, например,

• является ли вещество проводником или диэлектриком, какова его температура плавления и кипения, теплоёмкость и другие свойства;

• растворимость вещества в воде, способность вещества вступать в химические реакции.

Если изучаемое вещество планируется применять в качестве лекарства, то для него можно оценивать:

• лечебный эффект, способность связываться с определёнными патогенами в организме;

• токсичность для человека и возможные побочные эффекты;

• скорость распространения вещества в организме и выведения из него;

• степень взаимодействия с другими препаратами и риск аллергической реакции.

Более сложные задачи

Используя признаки, предсказанные для графа целиком, а также для его отдельных узлов и рёбер, можно решать и более продвинутые задачи, перечисленные ниже.

Компьютерная сеть

Интернет или внутреннюю сеть (intranet) можно описать в виде графа, где узлами выступают сетевые устройства, а рёбра проводятся, если между устройствами устанавливаются сетевые соединения.

Тогда можно решать следующие задачи:

• оценка пропускной способности определённых участков сети;

• оптимизация маршрутов передачи данных;

• обнаружение аномалий (взломов, атак, действий вредоносного ПО).

Городское планирование и транспорт

Пассажиропоток можно описать в виде транспортного графа (transportation network), в котором узлами будут остановки, перекрёстки, станции, а рёбрами - маршруты между ними. Тогда можно решать следующие задачи:

• оптимизация транспортных потоков;

• прогнозирования пробок;

• планирования городских систем (размещение станций, прокладка новых маршрутов).

Рынки и логистика

Взаимодействие экономических агентов можно описать в виде графа, в котором узлами выступают производители сырья, а также производители промежуточных и финальных продуктов, дистрибьюторы, продавцы и покупатели. Рёбрам будут соответствовать обмен товарами и финансовые расчёты. Используя этот граф, можно

• оценивать кредитоспособность агента;

• управлять запасами на складе;

• прогнозировать логистические задержки поставок;

• оптимизировать цепочки поставок.

Граф знаний

По размеченным текстам (например, из википедии) можно построить граф знаний (knowledge graph), где узлами выступают персоны, компании и события, а рёбрами - характер их взаимодействия.

Ниже рассмотрен пример такого графа для музеев, картин и художников [1]:

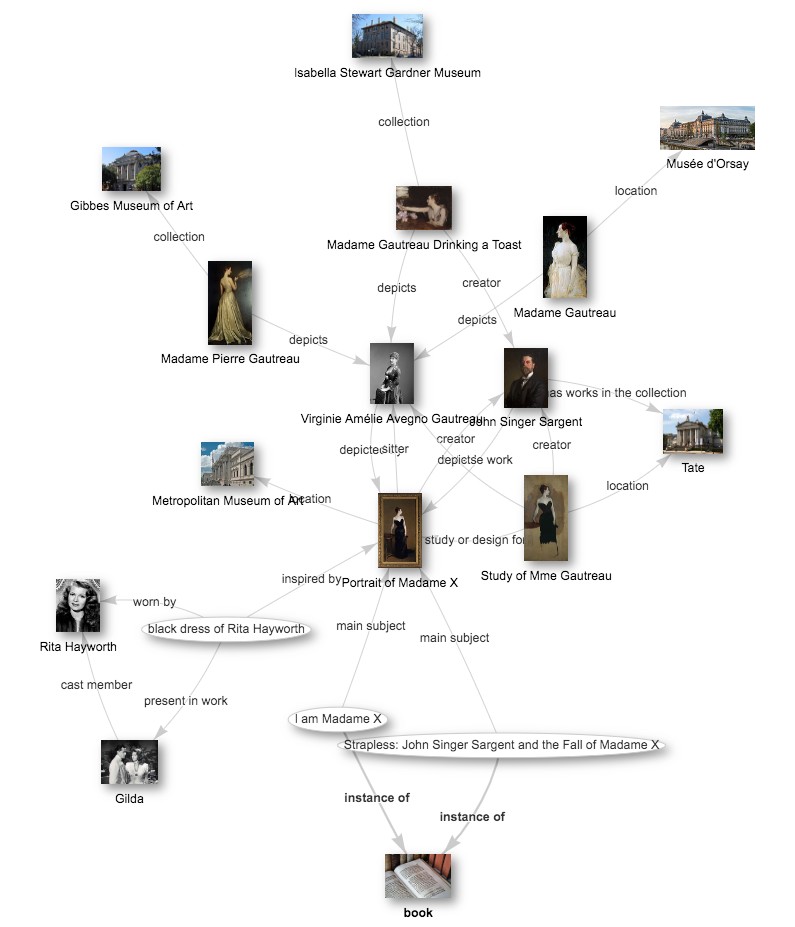
Примерами задач на подобном графе могут выступать:

• поиск опосредованных связей между персонами или событиями;

• оценка важности того или иного события в контексте поискового запроса;

• группировка людей, сообществ, событий по темам;

• объединение набора разрозненных фактов в целостные события.

Используя инструменты автоматического анализа, граф знаний можно составлять и из неструктурированного текста, а также из изображений, как показано ниже [2]:

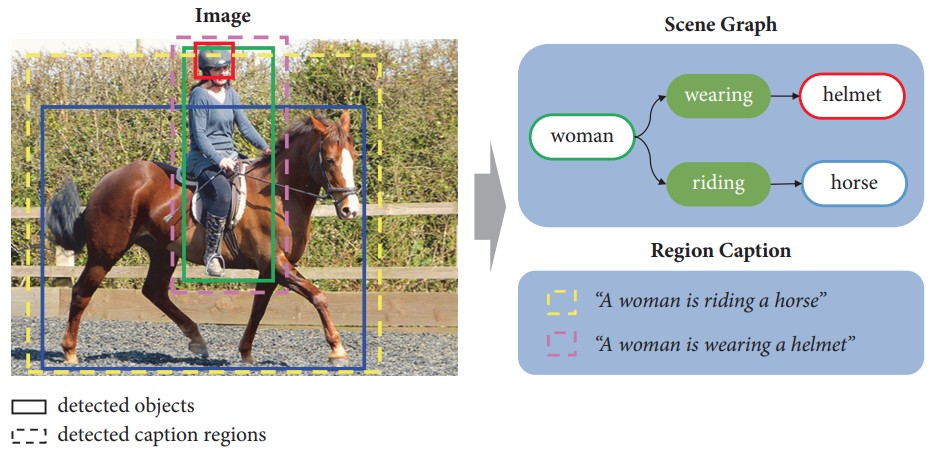
Программный код

Можно представить программный код в виде графа (control flow graph, call graph), в котором узлами будут функции, между которыми проводится ребро, если одна функция вызывает внутри себя другую. Либо узлами могут выступать переменные, а рёбрами - участие одних переменных в формировании других переменных (вычислительный граф). На подобных графах можно решать следующие задачи:

• определение избыточного кода, выявление участков, выполняющих одинаковые действия;

• обнаружение ошибок и уязвимостей;

• объяснение и автоматическое комментирование кода;

• генерация кода, дополняющего уже имеющийся;

• семантический поиск по коду - обнаружение всех участков кода, выполняющих определённый характер действий;

• анализ полноты покрытия кода проверочными тестами, автоматическое создание новых тестов.

---

Далее мы рассмотрим, как можно формализовать основные виды задач на графах, используя нейросети, а также изучим основной нейросетевой алгоритм - свёрточные графовые сети.

Литература

1. https://www.wikidata.org/wiki/User:Fuzheado/queries
2. Shin D., Kim I. Deep image understanding using multilayered contexts //Mathematical Problems in Engineering. – 2018. – Т. 2018. – №. 1. – С. 5847460.