Жадный и лучевой поиск

Введение

Рассмотрим, как можно улучшить качество текста, генерируемого последовательно слово за словом некоторой моделью, такой как рекуррентная сеть.

Предложенный метод имеет более широкую применимость. В частности, он может применяться:

• к любым языковым моделям, например, трансформерам;

• к генерации любых дискретных объектов (ДНК как последовательности нуклеотидов; сессии как последовательности действий пользователя на сайте и т.д.).

Сеть генерирует текст последовательно слово за словом среди $V$ уникальных слов словаря. На каждом шаге сеть выдаёт $V$ рейтингов каждого отдельного слова (или символа при посимвольной генерации):

$$\hat{r}=[\hat{r}_1,\hat{r}_2,...\hat{r}_V]=f(\mathbf{x}_t,\mathbf{h}_t)$$

Эти рейтинги преобразуются в вероятности слов, используя SoftMax-преобразование:

$$\text{SoftMax}_{\tau}\left(\widehat{r}_{1},...\widehat{r}_{V}\right)=\frac{1}{\sum_{i}e^{\widehat{r}_{i}/\tau}}\cdot\left(\begin{array}{c} e^{\widehat{r}_{1}/\tau}\\ e^{\widehat{r}_{2}/\tau}\\ \cdots\\ e^{\widehat{r}_{V}/\tau} \end{array}\right),$$ $$\tau>0 - \text{гиперпараметр температуры.}$$

Нас интересует генерация последовательности слов, обладающая максимальным рейтингом (который является некоторой функцией от модельного правдоподобия сгенерированной последовательности слов).

Вначале рассмотрим работу более простого алгоритма жадного поиска (greedy search), а затем опишем работу более продвинутого лучевого поиска (beam search), осуществляющего более полный перебор.

Алгоритм жадного поиска

Простейший подход генерации слов или символов текста - генерировать каждый раз следующее слово (или символ), дающее наивысший рейтинг последовательности. Этот подход называется жадным поиском (greedy search).

Пример работы

Пусть, для простоты, генерация происходит не на уровне слов, а на уровне букв, причем рассматриваются только две буквы: "A" и "M". Нам нужно сгенерировать слово из четырёх букв словаря, обладающего максимальным рейтингом $S(\cdot)$:

$$\arg\max_{c_1c_2c_3c_4} S(c_1c_2c_3c_4) - ?$$

В качестве рейтинга используется некоторое преобразование от модельной вероятности пронаблюдать именно такую цепочку символов в последовательности:

$$P(c_1c_2c_3c_4)=P(c_1)P(c_2|c_1)P(c_3|c_1c_2)P(c_4|c_1c_2c_3)$$

Процесс итеративного построения слова можно представить в виде дерева, каждый узел которого отвечает некоторому варианту выбранного слова с приписанным ему рейтингом.

Нулевой ярус дерева отвечает пустому слову, первый - слову из одной буквы ("A" или "M"), следующий - слову из двух букв ("AA", "AM", "MA", "MM") и т. д.

Поскольку нужно составить наилучшее слово из четырёх букв, нам требуется найти узел четвёртого яруса дерева, обладающий максимальным рейтингом.

Ниже представлен пример дерева выбора с рейтингами узлов:

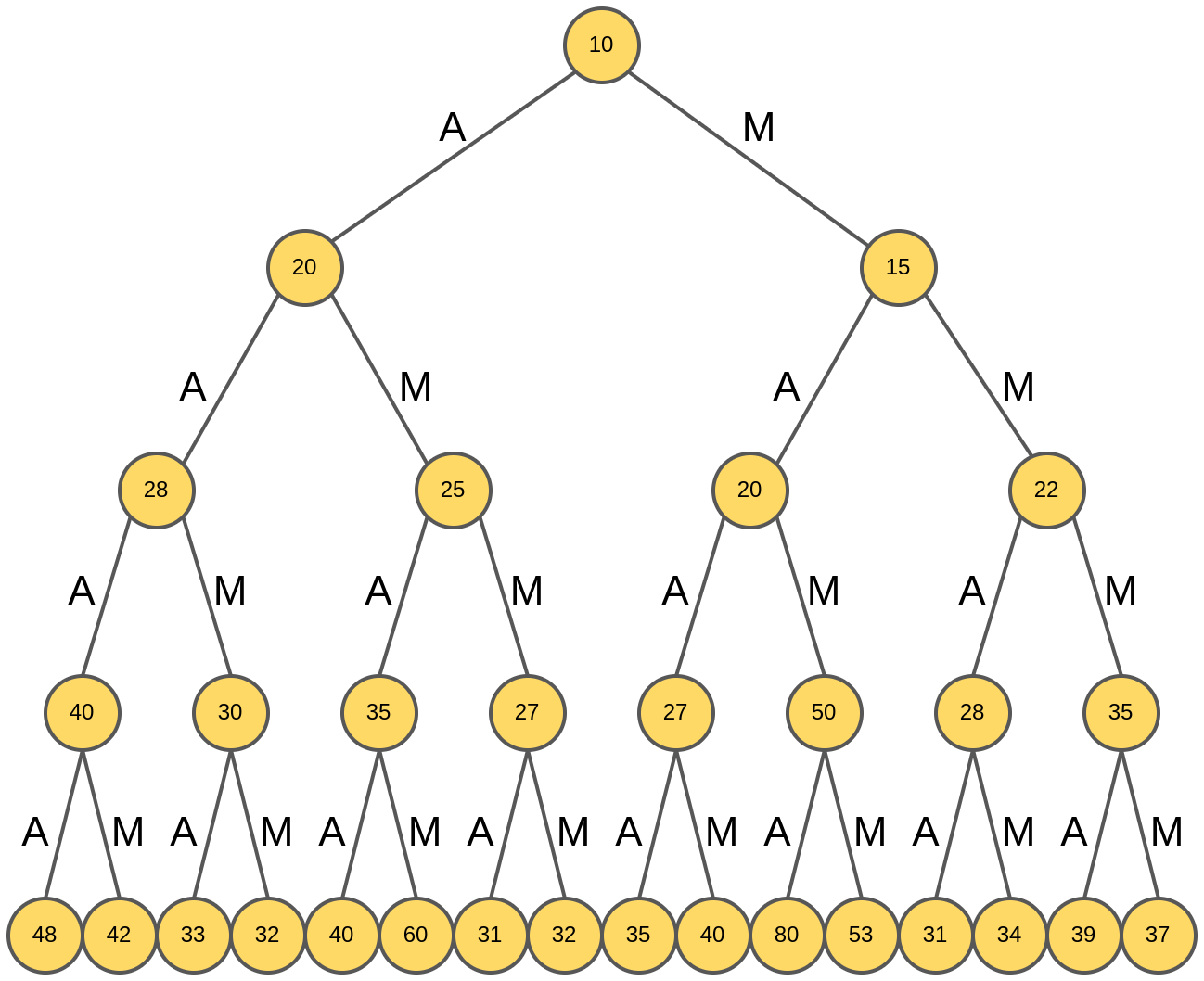
Генерация жадного поиска стартует из корня дерева (отвечающего пустому слову), и анализируются рейтинги слов из одной буквы:

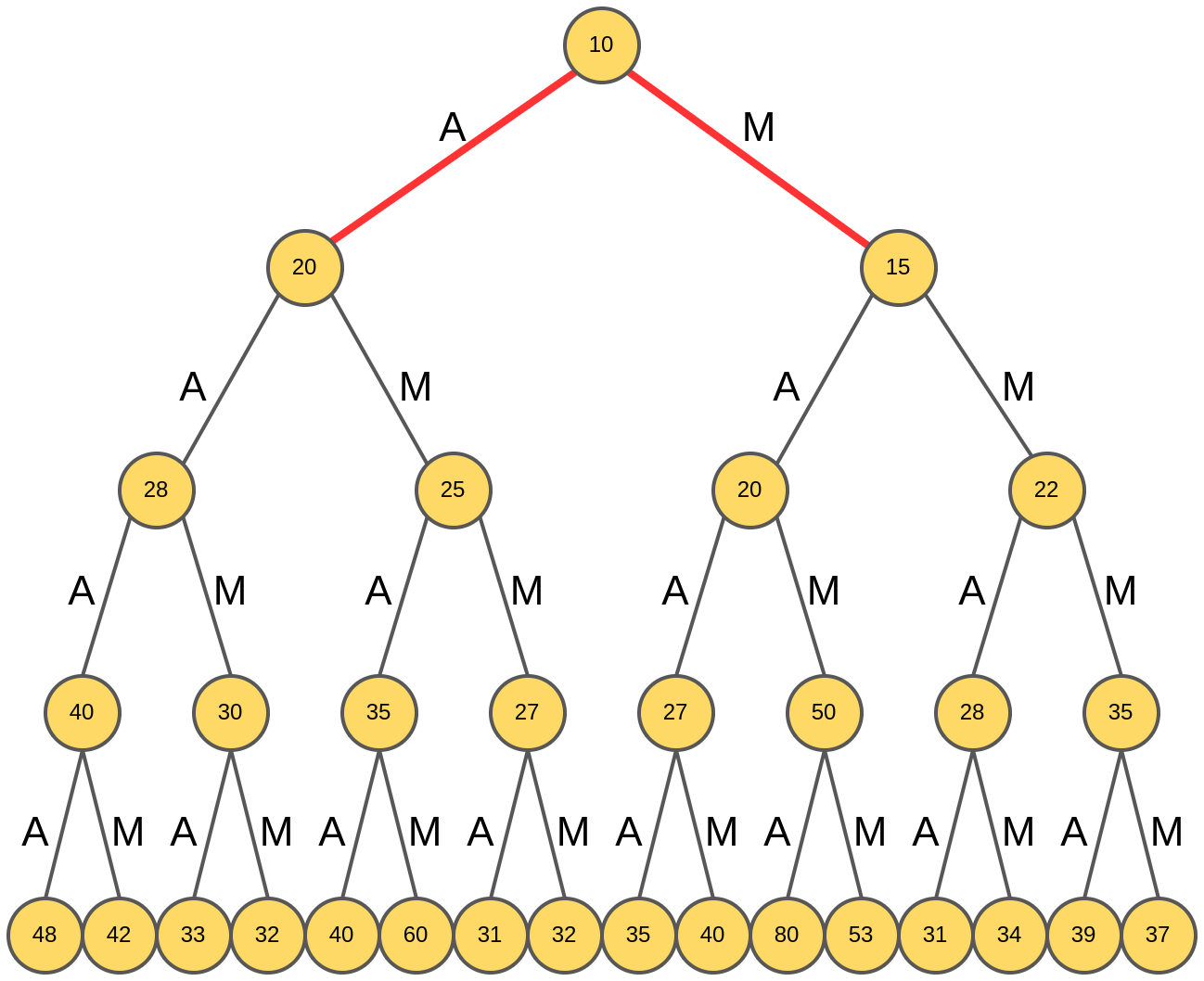
Выбирается слово "A", обладающее максимальным рейтингом 20.

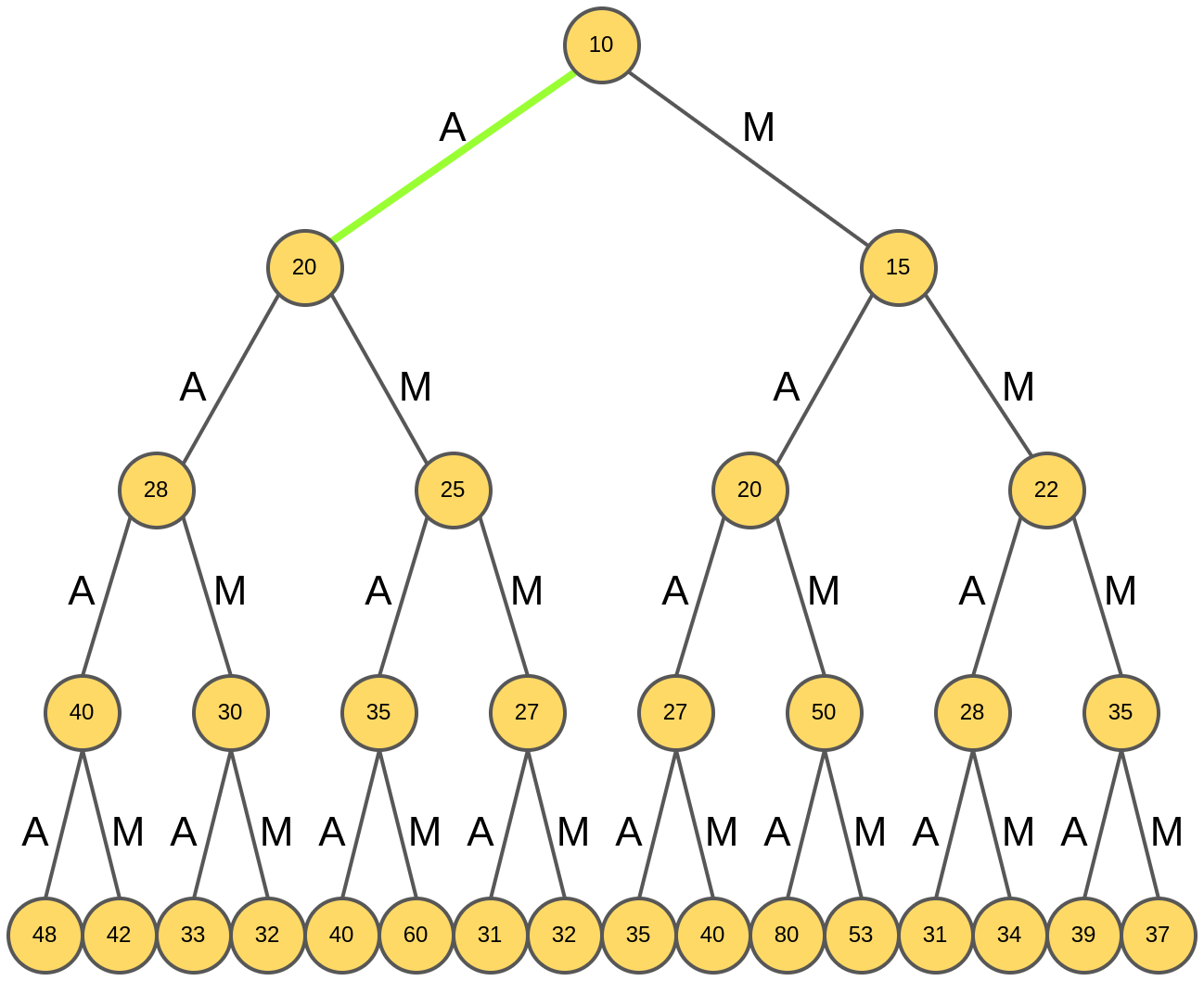
Далее для префикса "А" анализируются продолжения "AA" и "AM".

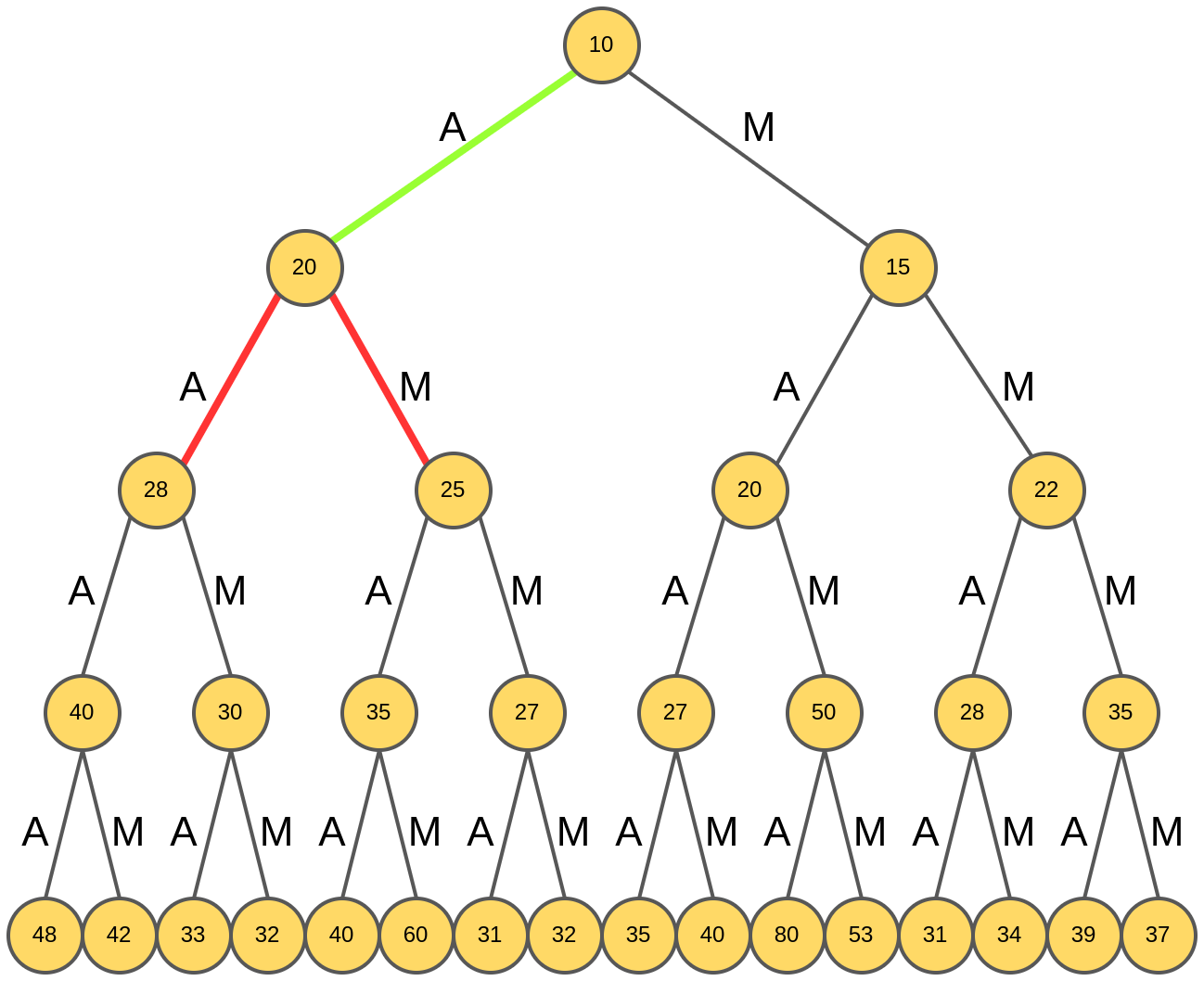
Выбирается "AM", обладающее максимальным рейтингом.

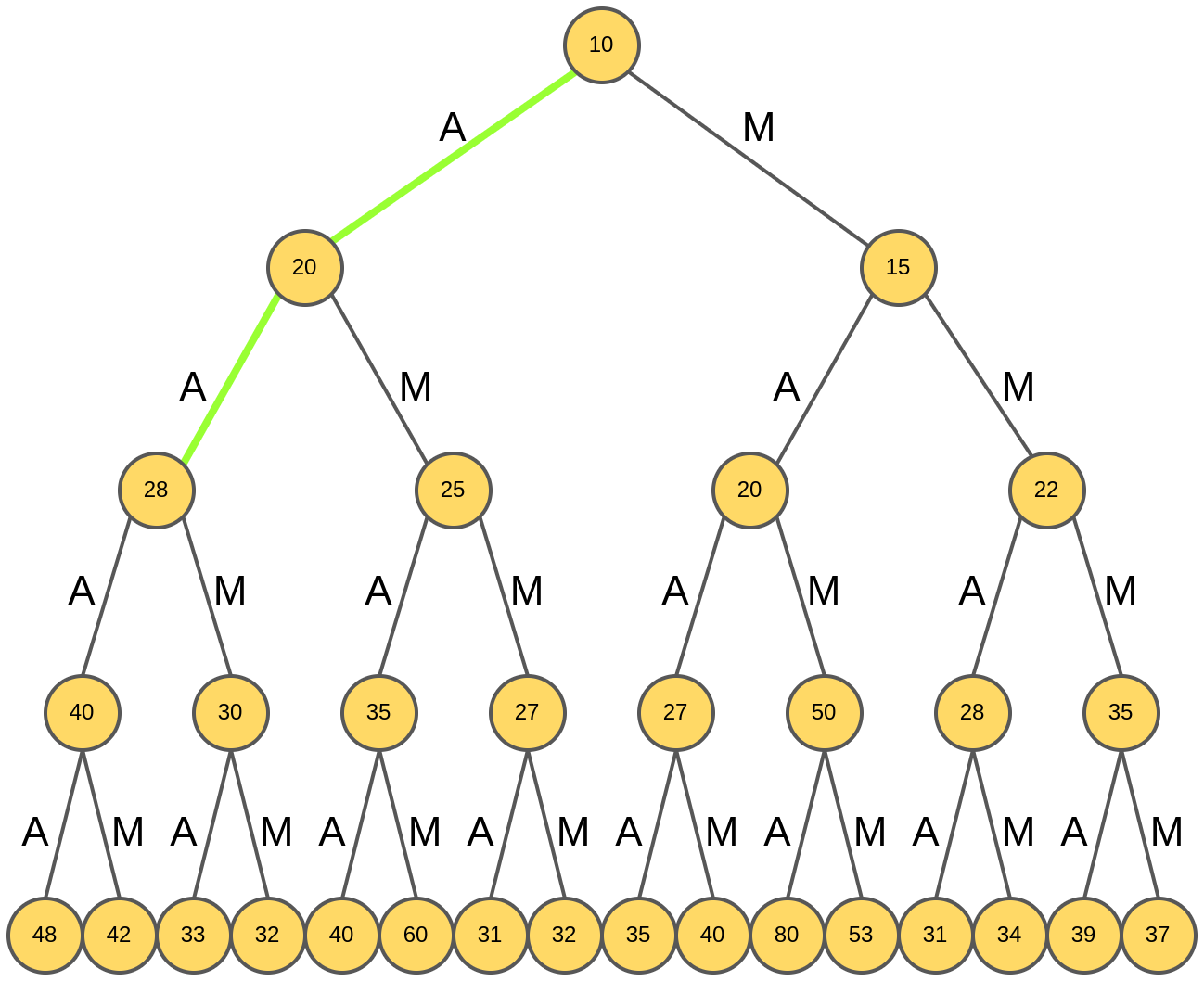
Далее снова анализируются возможные продолжения "AA": "AAA" и "AAM":

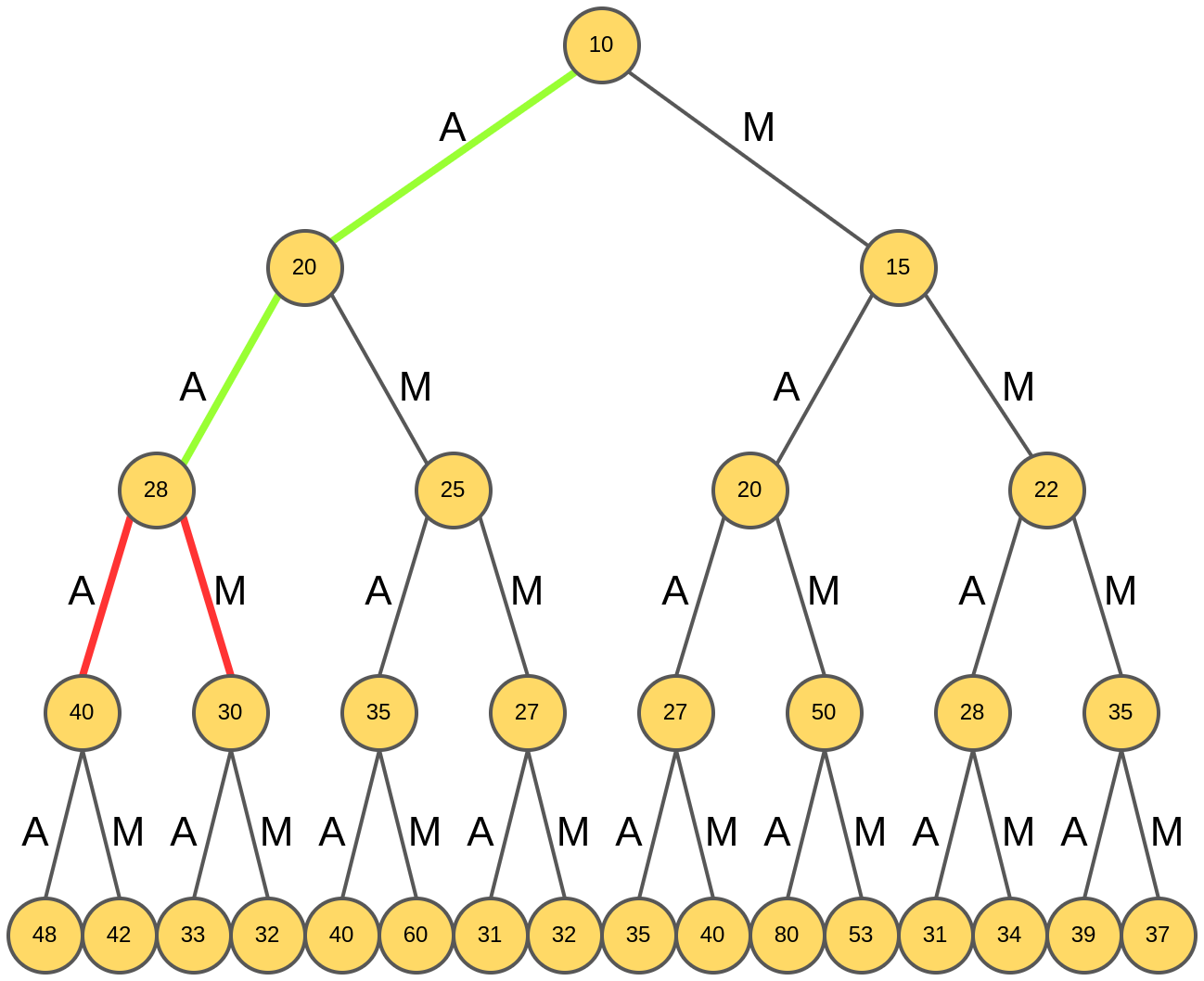
Выбирается префикс "AAA":

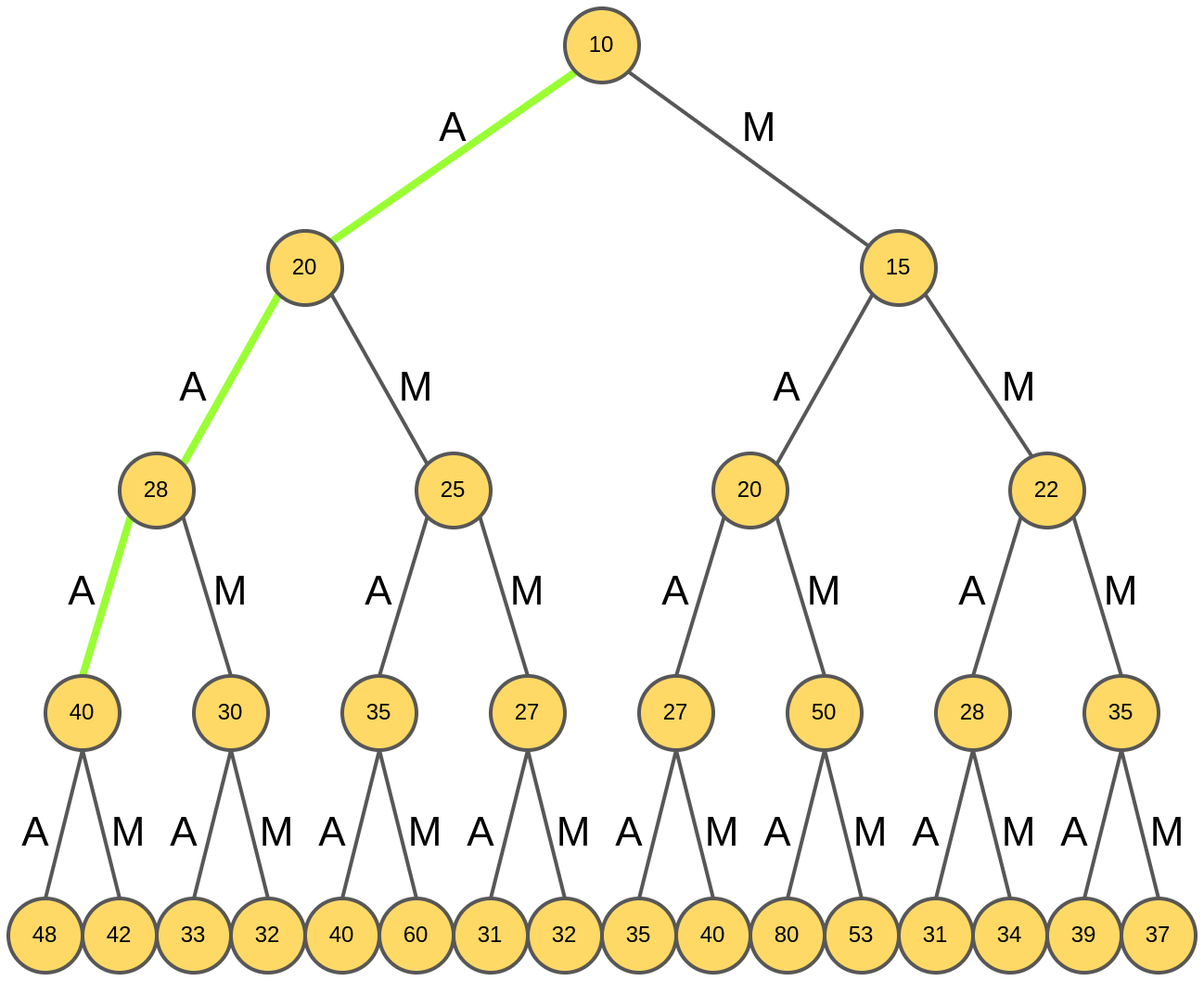
Для "AAA" снова анализируются продолжения: "AAAA" и "AAAM":

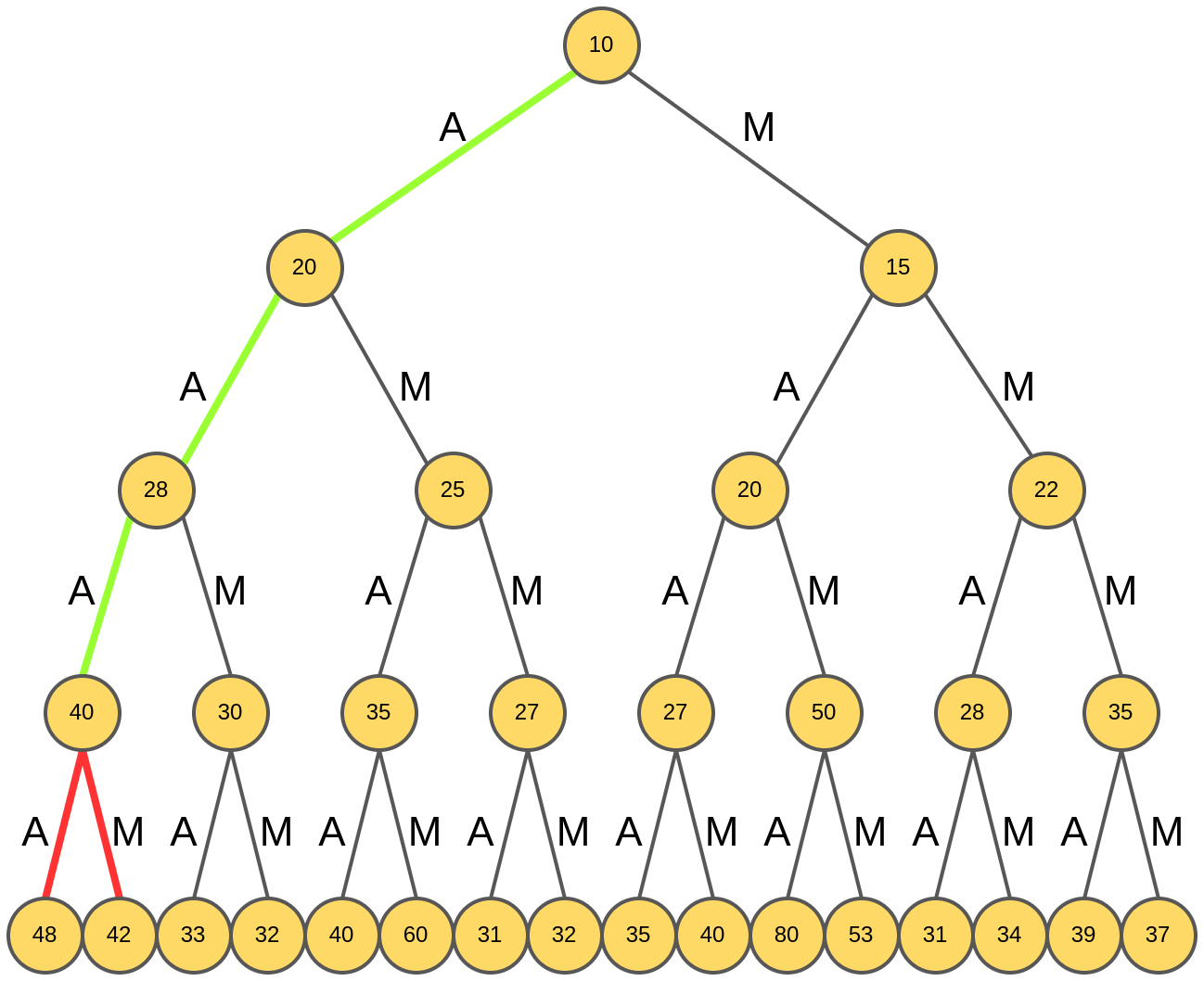
Выбирается слово "AAAA", и на этом генерация четырёхбуквенного слова завершается:

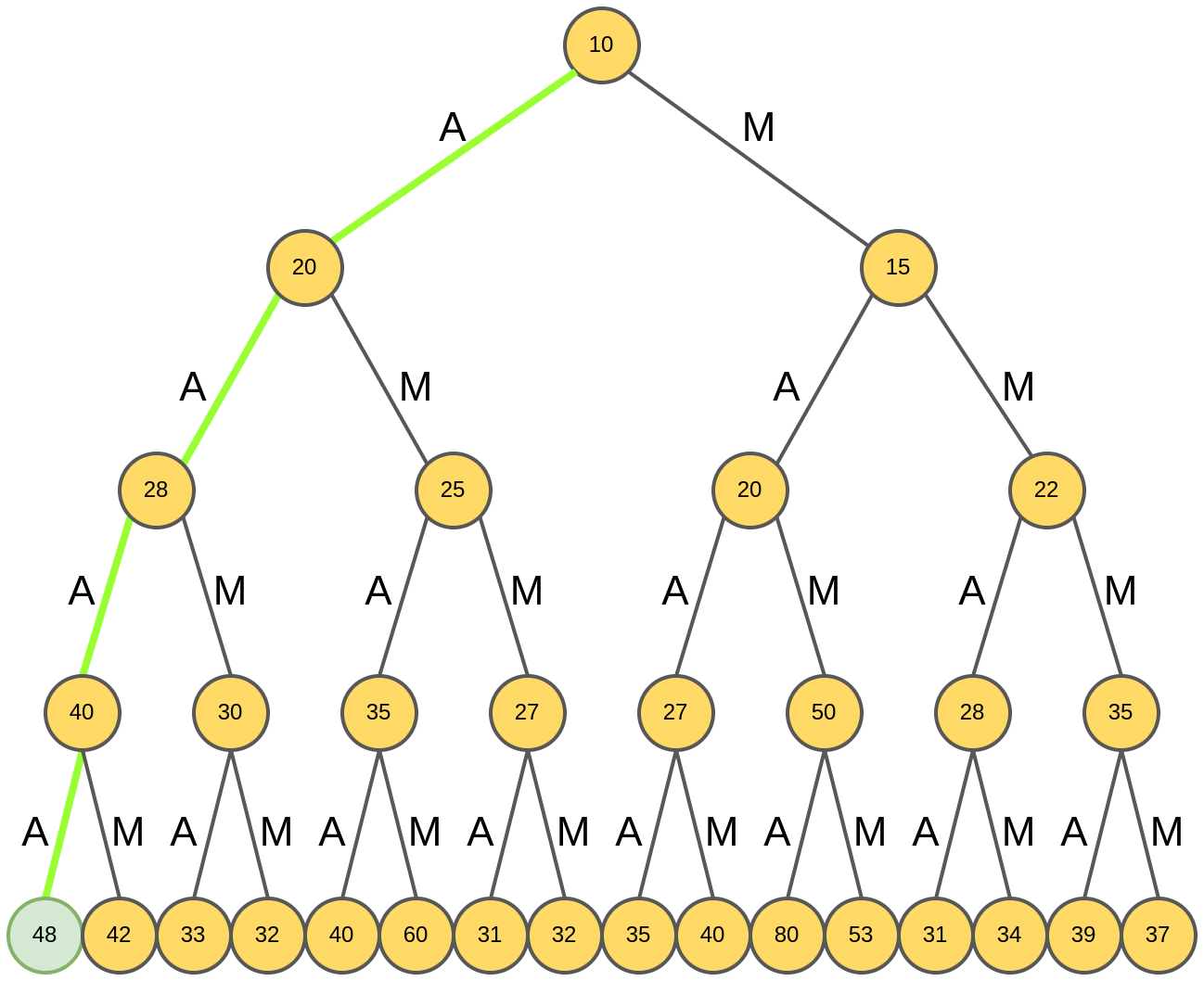
Полученное слово "AAAA" обладает рейтингом 48.

Алгоритм лучевого поиска

Поскольку каждый раз алгоритм смотрит только на один шаг вперёд, то сгенерированная последовательность как целое может оказаться неоптимальной, то есть обладающей недостаточно высоким рейтингом $S(c_1c_2...c_T)$ по сравнению с альтернативными вариантами.

Для повышения качества сгенерированных последовательностей используется лучевой поиск (beam search), суть которого состоит в том, что выбирается каждый раз не одна гипотеза, а набор из K лучших гипотез, где $K$ - гиперпараметр метода. Получив $K$ итоговых последовательностей, можно среди них выбрать ту, которая обладает максимальным рейтингом, что обеспечит более полный перебор вариантов.

Пример работы

Опишем алгоритм визуально для примера выше (генерация четырёхбуквенного слова из букв "A" и "M"), когда $K=2$, т.е. параллельно дорабатываются две лучших гипотезы.

Генерация лучевого поиска стартует из корня дерева (отвечающего пустому слову) и анализируются рейтинги слов из одной буквы:

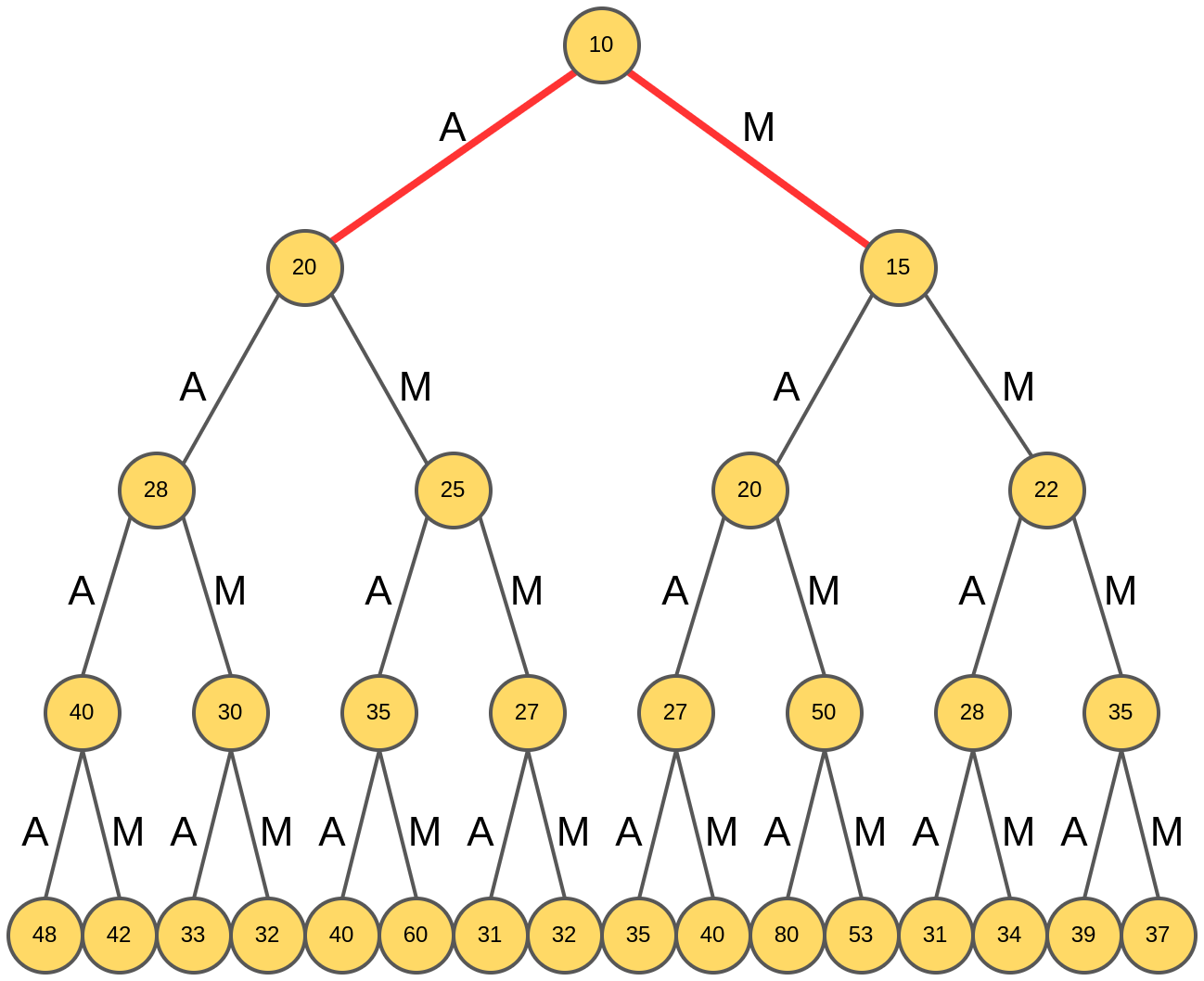
В отличие от жадного поиска, лучевой поиск идёт одновременно по двум маршрутам, используя гипотезы "A" и "M":

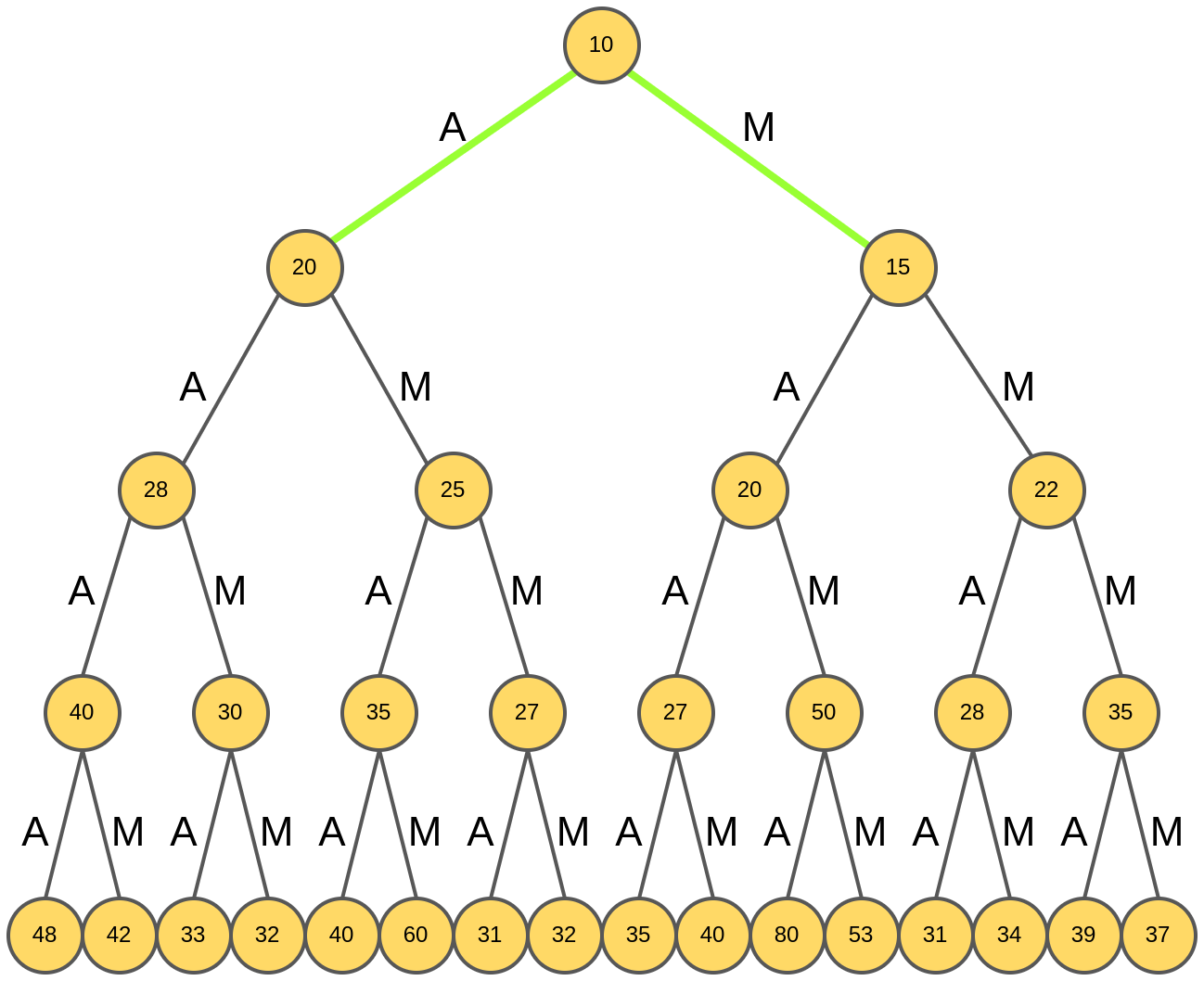
Для каждой гипотезы анализируются их всевозможные расширения:

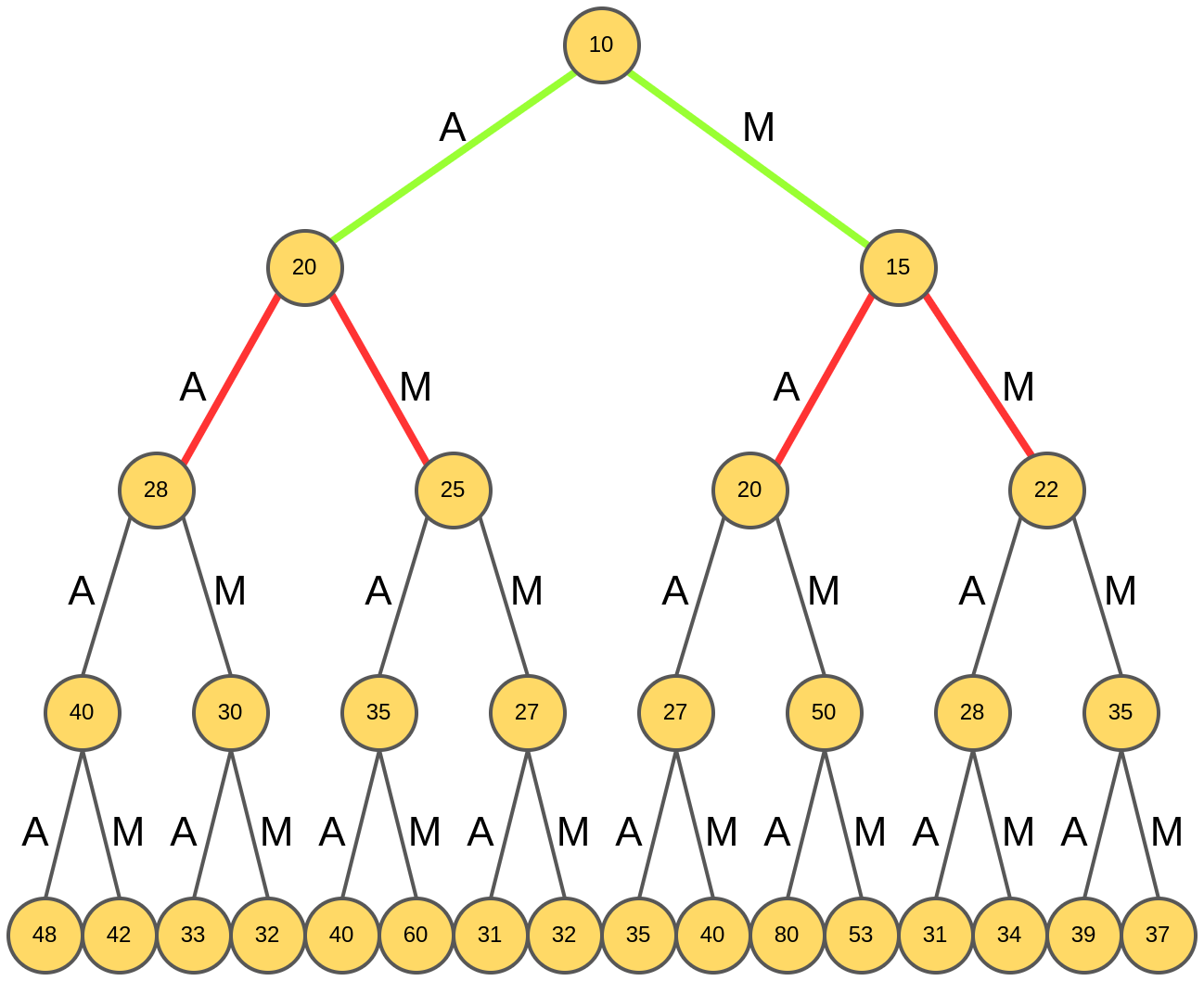
Наилучшими оказались гипотезы "AA" и "AM", префикс "M" отбрасывается как обеспечивающий расширение с меньшим рейтингом:

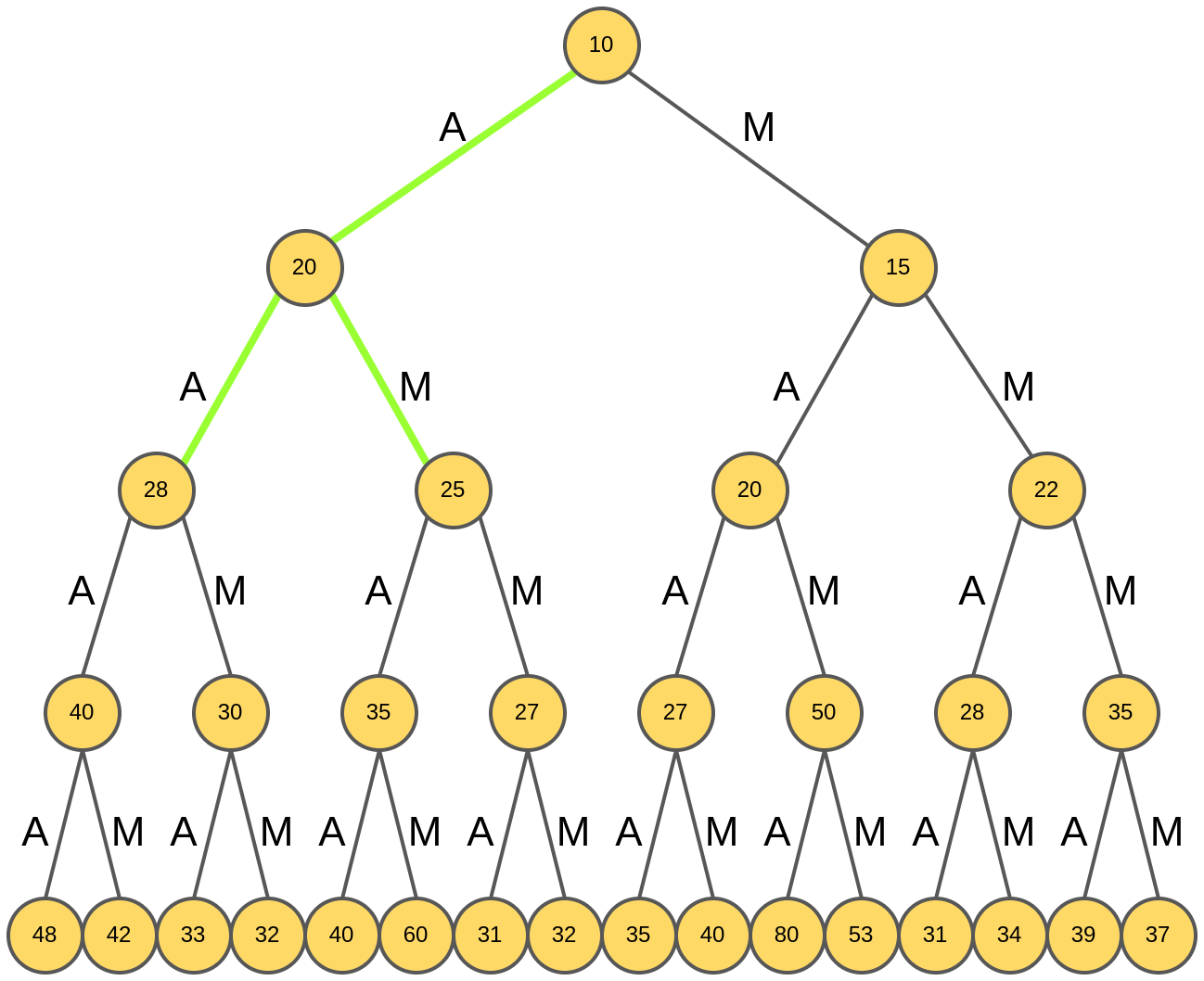
Снова анализируются продолжения каждой из двух гипотез:

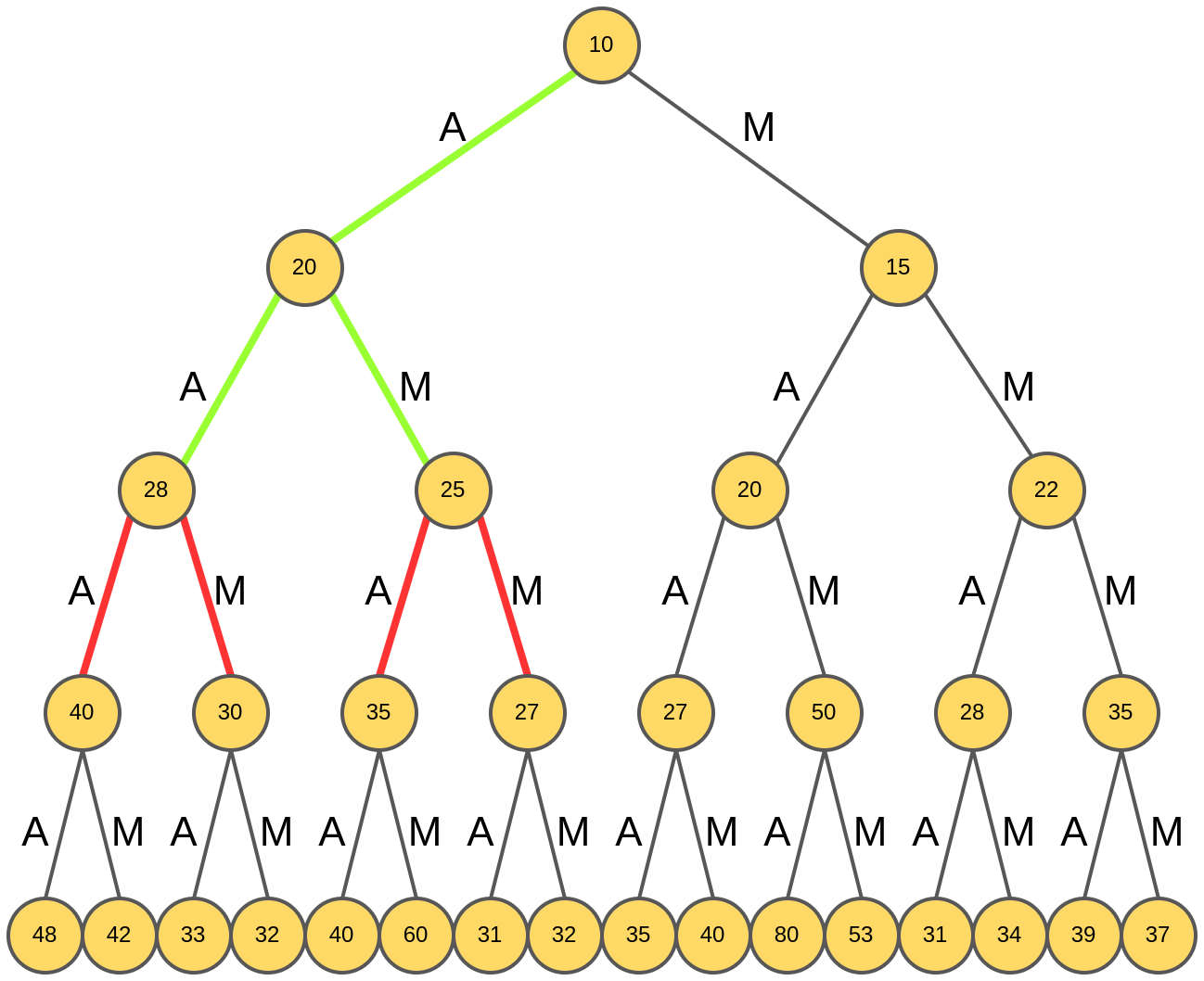
Лучшими продолжениями оказываются "AAA" и "AMA":

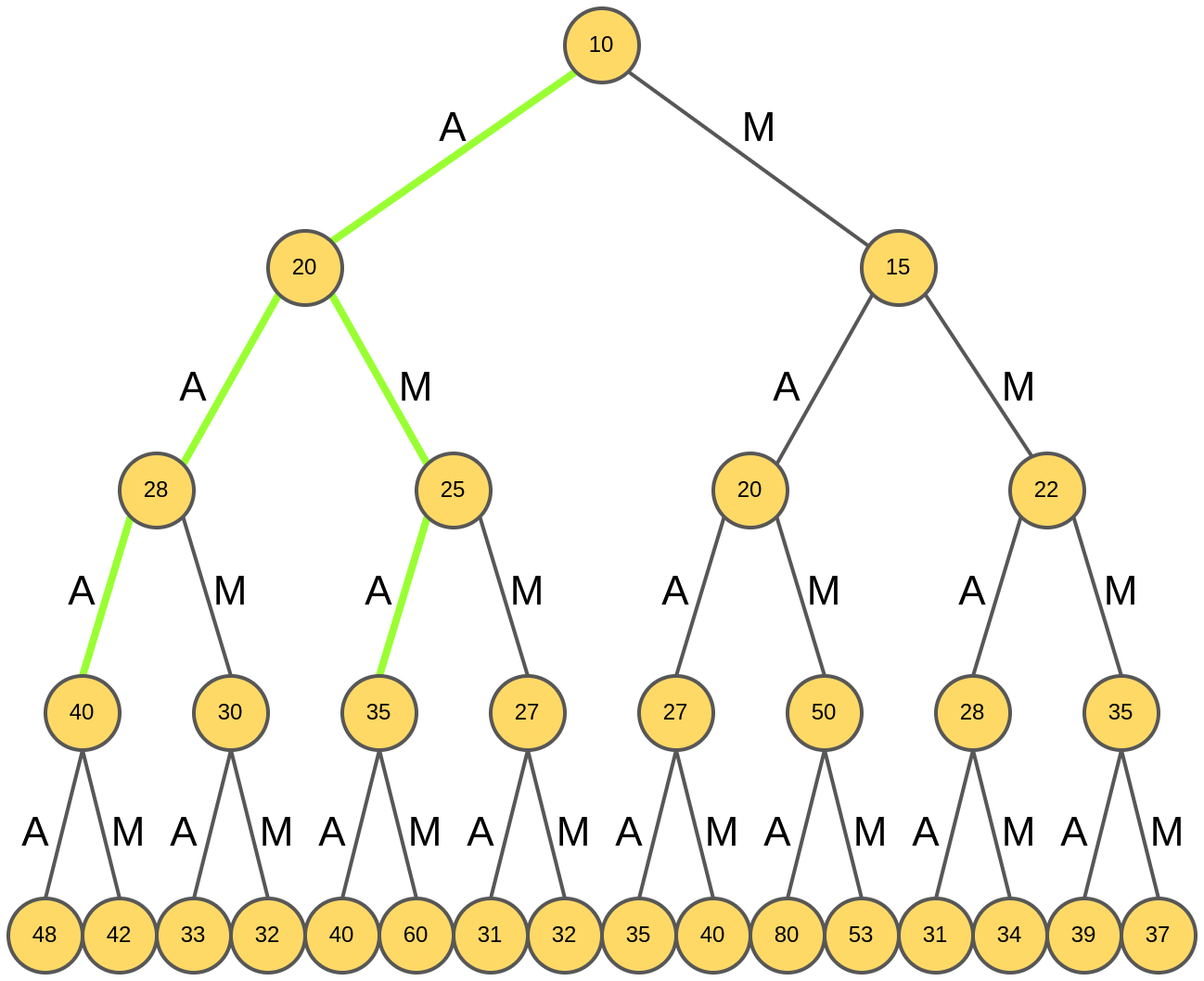
Анализируются продолжения этих гипотез:

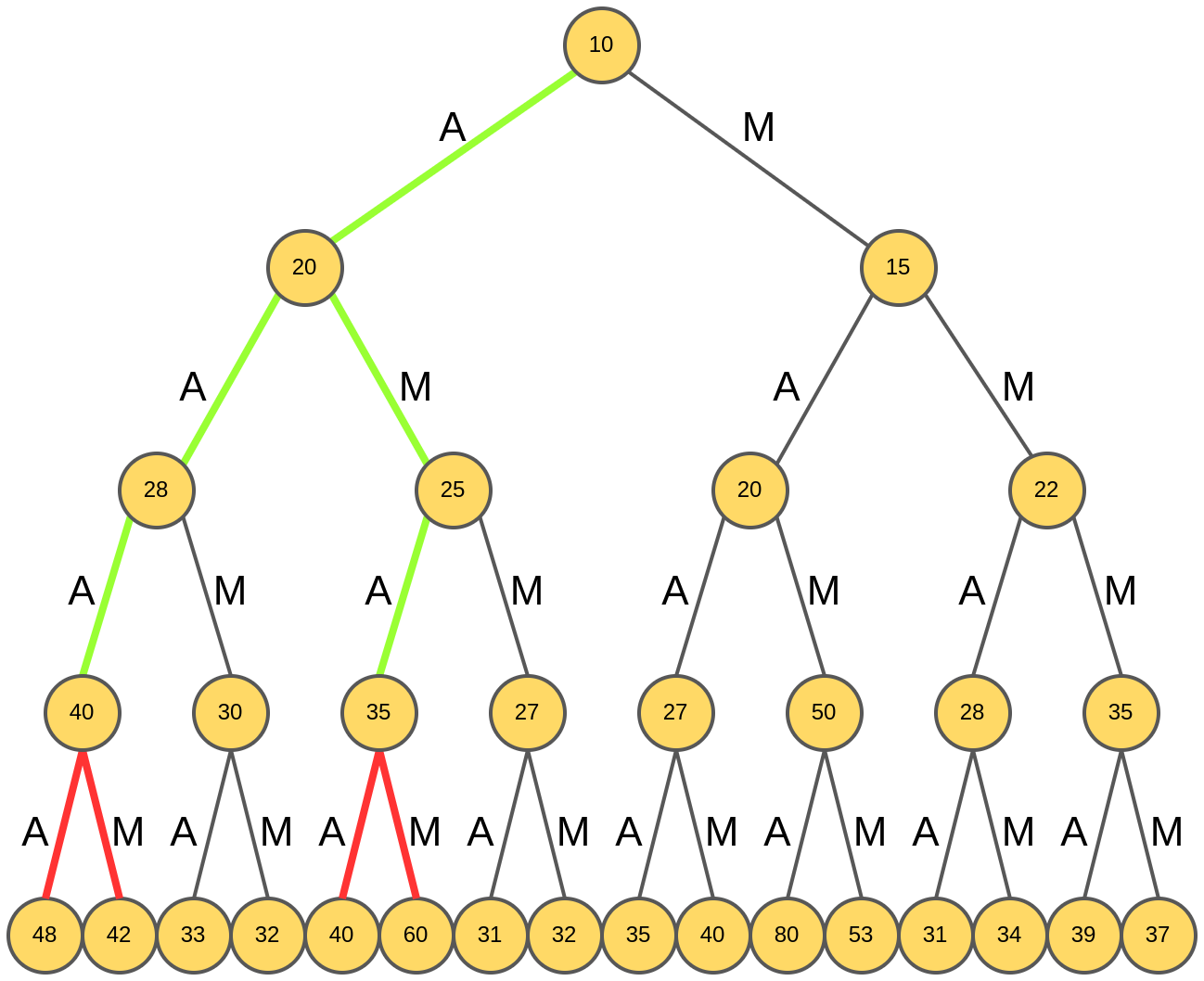
Выбираются две лучших - "AAAA" и "AMAM" с рейтингами 48 и 60:

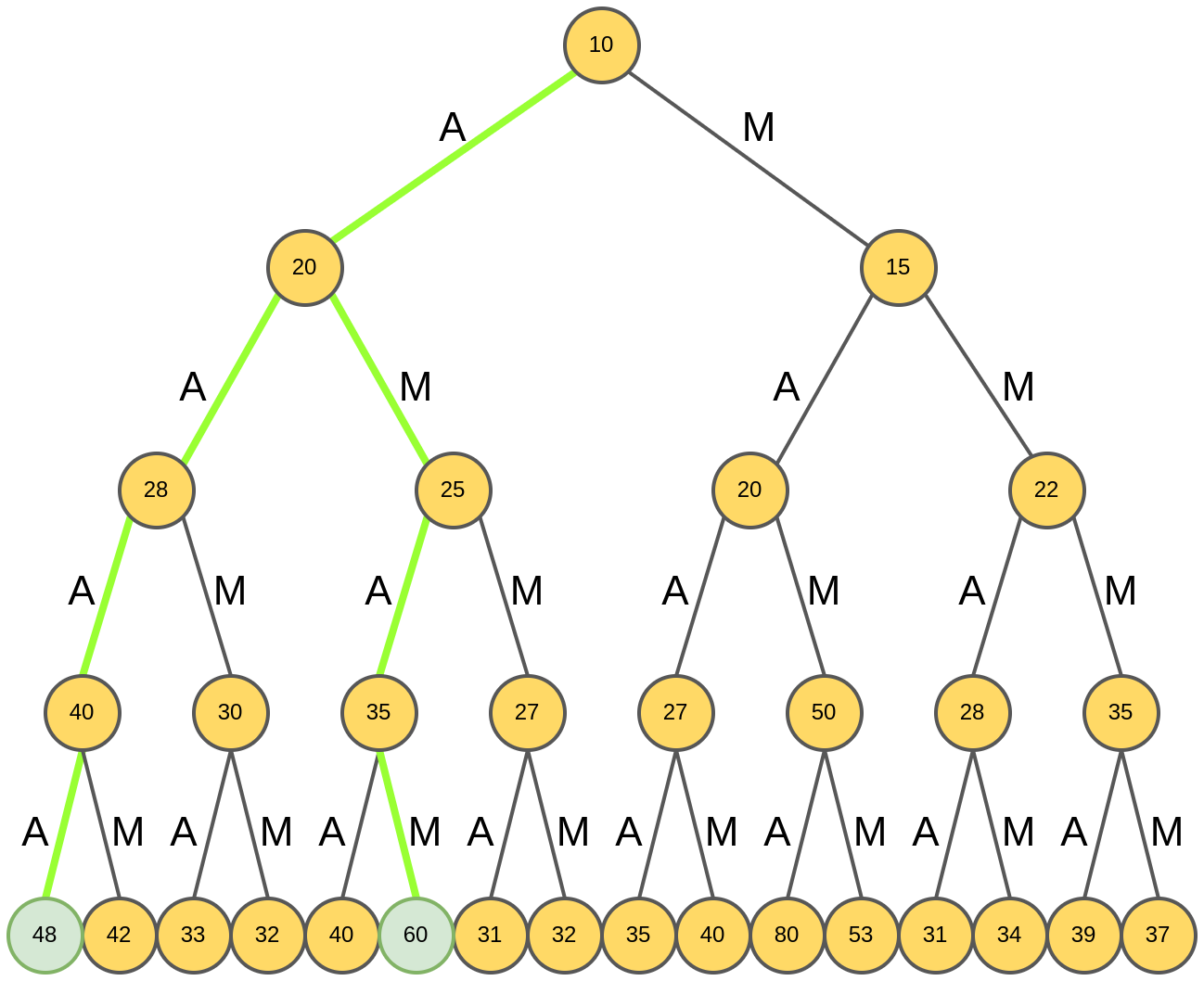
Итоговой генерацией будет слово "AMAM", обладающее максимальным рейтингом среди отобранных на предыдущем шаге.

За счёт расширения пространства поиска нам удалось сгенерировать слово с более высоким рейтингом (60), чем при использовании жадного поиска (48)!

Анализ лучевого поиска

Обратим внимание, что лучевой поиск всё же не обеспечивает полный перебор. Из-за этого мы упустили наилучшую генерацию слова "MAMA" с рейтингом 80:

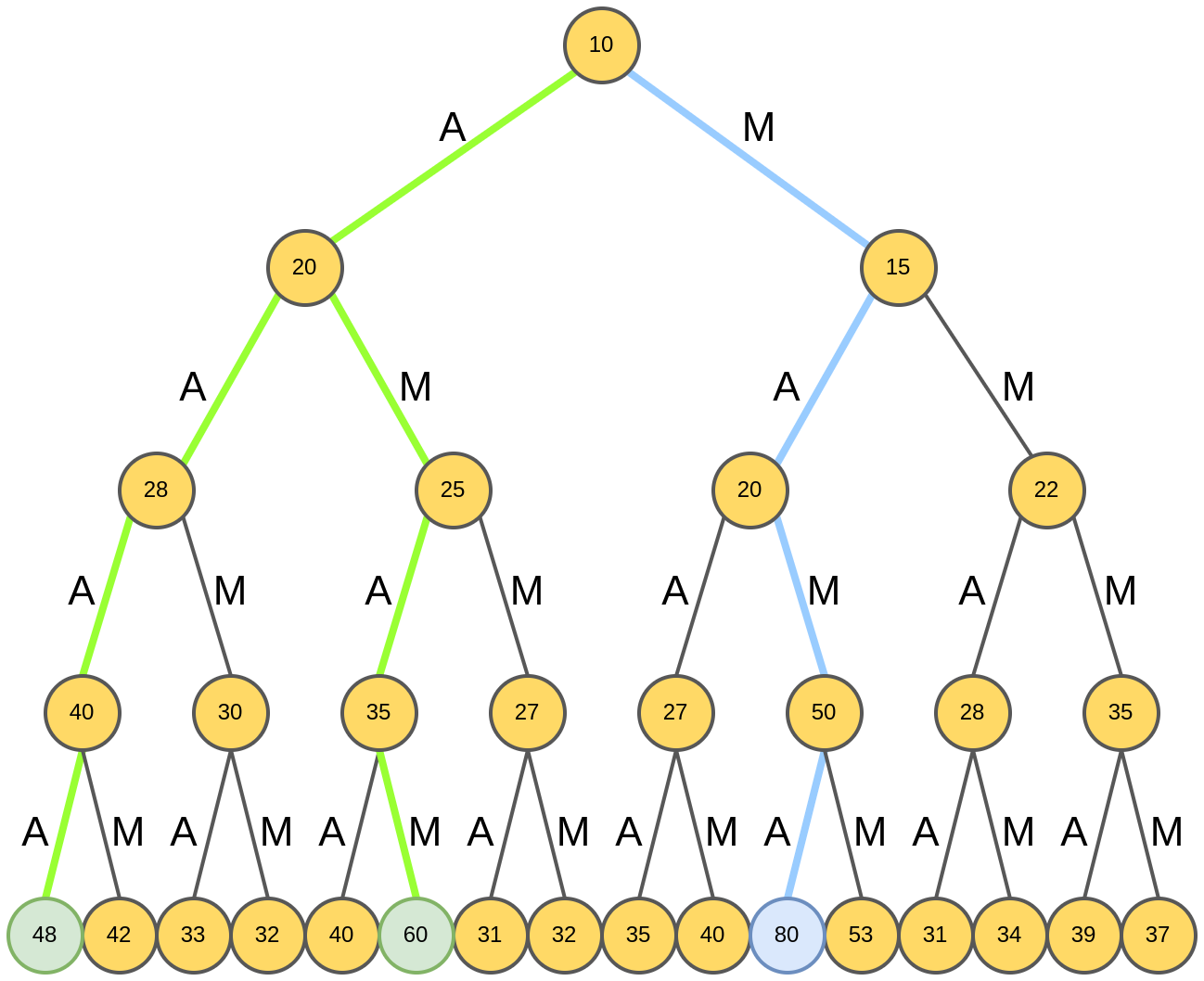
При $K=1$ лучевой поиск сводится к жадному алгоритму. Чем гиперпараметр $K$ выше, тем шире пространство перебора, и тем больше шансов найти не локально, а глобально оптимальное решение.

При $K\ge V^T$, где $V$ - объём словаря, а $T$ - длина генерируемой последовательности, лучевой поиск сведётся к полному перебору (full search).

Случайная генерация

Если в языковом моделировании выбирать слова, обладающие максимальной вероятностью, то это часто будет приводить к генерации очень правильных, но слишком однообразных текстов, склонных к зацикливанию.

Чтобы этого не происходило, слова рекомендуется сэмлировать из распределения, предсказанного моделью, причём гиперпараметр температуры $\tau>0$ в SoftMax-преобразовании управляет контрастностью выходных вероятностей.

Как именно?

При $\tau\to 0$ сэмплирование по-прежнему сводится к выбору самого вероятного слова и генерирует текст, который будет максимально правильным, но слишком однообразным. Увеличение $\tau$ повышает разнообразие ценой уменьшения согласованности слов в тексте (или букв в случае посимвольной генерации).

Таким образом, стохастическая генерация последовательности слов (или других дискретных элементов) в рекуррентной сети происходит пошагово генерируя последовательно слово за словом:

1. $w_1\sim p_\tau(w)$,

2. $w_2\sim p_\tau(w|w_1)$,

3. $w_3\sim p_\tau(w|w_1w_2)$,

4. $w_4\sim p_\tau(w|w_1w_2w_3)$

    и т. д.

При этом, чтобы уменьшить риск генерации случайного слова, которое будет совсем выпадать из контекста, слова генерируют не из всего списка слов, а из подмножества максимально вероятных. Для этого есть два подхода:

• Top-K sampling позволяет сэмплировать только $K$ слов, обладающих максимальной вероятностью.

• Nucleus sampling: вместо задания $K$ задаётся пороговая вероятность $P$. Слова генерируются не из всего списка, а из подмножества самых вероятных слов. Оно формируется следующим образом: слова сортируются по убыванию их вероятности, и в допустимое подмножество включается минимальное число топ-K самых вероятных слов так, что их суммарная вероятность стала выше $P$. Таким образом, Nucleus sampling представляет собой разновидность top-K sampling с динамически изменяемым параметром K, адаптивно подстраиваемым под контекст.

Генерация слов продолжается, пока не будет сгенерирован специальный токен [EOS], означающий конец последовательности, либо пока вероятность окончания генерации (предсказываемая отдельным выходом сети) не превысит порог.

Рейтинг последовательности

При генерации последовательности слов $w_1w_2...w_T$ можно по-разному оценивать её качество. Например, использовать логарифм модельной вероятности сгенерированной цепочки:

$$\begin{aligned} S(w_1w_2...w_T) &= \log P(w_1w_2...w_T) \\ &=\log P(w_1)P(w_2|w_1)...P(w_T|w_1w_2...w_{T-1}) \\ &=\sum_{t=1}^T \log P(w_t|w_1w_2...w_{t-1}), \\ \end{aligned}$$

однако такой способ будет поощрять более короткие последовательности как приводящие к меньшему числу произведений малых вероятностей. Чтобы простимулировать нейросеть генерировать более длинные варианты текста, рейтинг нормируют на длину выходной последовательности по формуле

$$\begin{aligned} S(w_1w_2...w_T) = \frac{1}{T^\alpha}\sum_{t=1}^T \log P(w_t|w_1w_2...w_{t-1}), \end{aligned}$$

где $\alpha\sim 0.75$ - гиперпараметр, управляющий предпочтительной длиной выходных последовательностей.

Как именно?

При уменьшении $\alpha$ рейтинг длинных последовательностей будет получаться выше, и они будут выбираться чаще.

В расчёт рейтинга также можно добавлять другие условия, измеряющие, насколько сгенерированный текст

• разнообразен (содержит много уникальных $n$-грамм);

• естественен (содержит длинные последовательности слов, которые реально встречаются в текстах).

Литература

1. http://karpathy.github.io/2015/05/21/rnn-effectiveness/