Перейти к основному содержимому

Генерация последовательностей

Рекуррентную сеть можно использовать для генерации последовательности y^1y^2,...y^T\hat{\mathbf{y}}_1\hat{\mathbf{y}}_2,...\hat{\mathbf{y}}_T, которая может представлять собой:

  1. последовательность чисел (например, изменение температур);

  2. последовательность вещественных векторов (например, цены на акции завтра, послезавтра, и т.д.);

  3. последовательность дискретных объектов (например, цепочку слов при генерации текста).

Простая генерация (текстов, временных рядов) не имеет прикладного смысла. Однако большое значение имеет условная генерация (conditional generation), например, когда:

  • генерируется текст по заданной теме (ответ на вопрос);

  • генерируется временной ряд по условию (вероятная динамика будущих цен из текущей ситуации на рынке).

Поэтому безусловная генерация разрабатывается как предварительный этап перед условной генерацией в описанных далее архитектурах one-to-many и many-to-many.

Для этого в начале генерации сети подаётся некоторое фиксированное начальное состояние h0\mathbf{h}_0 и фиксированный вектор начального входа y^0\hat{\mathbf{y}}_0.

Их можно задавать как нулевые вектора или как обучаемые параметры, настраиваемые с другими весами модели.

Последующая генерация несколько различается в зависимости от того, генерируем ли мы вектора вещественных чисел или дискретные объекты, такие как слова текста.

Генерация векторов чисел​

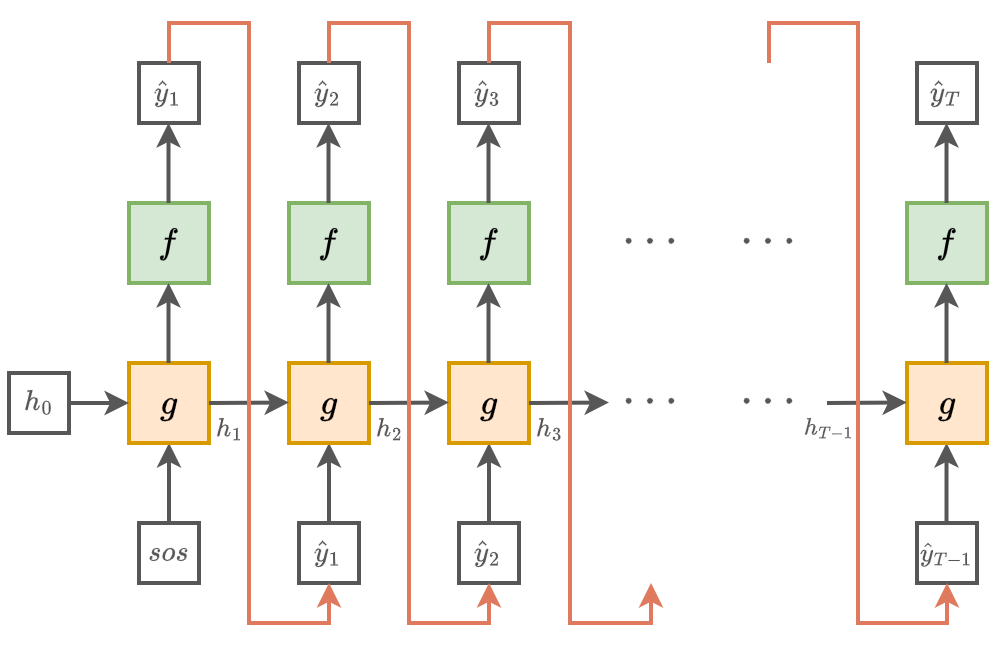
При генерации векторов вещественных чисел для t=1,2,3...t=1,2,3... сеть пересчитывает внутреннее состояние и выход, принимая на вход собственный выход в предыдущий момент времени. Вводится дополнительная функция pt=s(ht)p_t=s(\mathbf{h}_t), которая по внутреннему состоянию оценивает вероятность конца генерации ptp_t. Как только эта вероятность становится выше некоторого порогового значения, генерация останавливается.

Это формализуется в виде следующего алгоритма:

ЗАДАТЬ:

  • h0,y^0\mathbf{h}_0,\hat{\mathbf{y}}_0 (например, нулевыми векторами)
  • pmaxp_{max} (например, 0.9)

t:=0t:=0

ПОВТОРЯТЬ:

  • xt:=y^t−1\mathbf{x}_t:=\hat{\mathbf{y}}_{t-1}

  • ht:=g(xt,ht−1)\mathbf{h}_{t}:=g(\mathbf{x}_{t}, \mathbf{h}_{t-1})

  • y^t:=f(xt,ht)\hat{\mathbf{y}}_{t}:=f(\mathbf{x}_{t}, \mathbf{h}_{t}) 

  • pt:=s(ht)p_t:=s(\mathbf{h}_t)

ПОКА pt<pmaxp_t<p_{max}   

ВЫХОД:

  • последовательность y^1y^2...y^t\hat{\mathbf{y}}_1 \hat{\mathbf{y}}_2 ... \hat{\mathbf{y}}_t

Графически указанный процесс генерации показан ниже:

Генерация дискретных объектов​

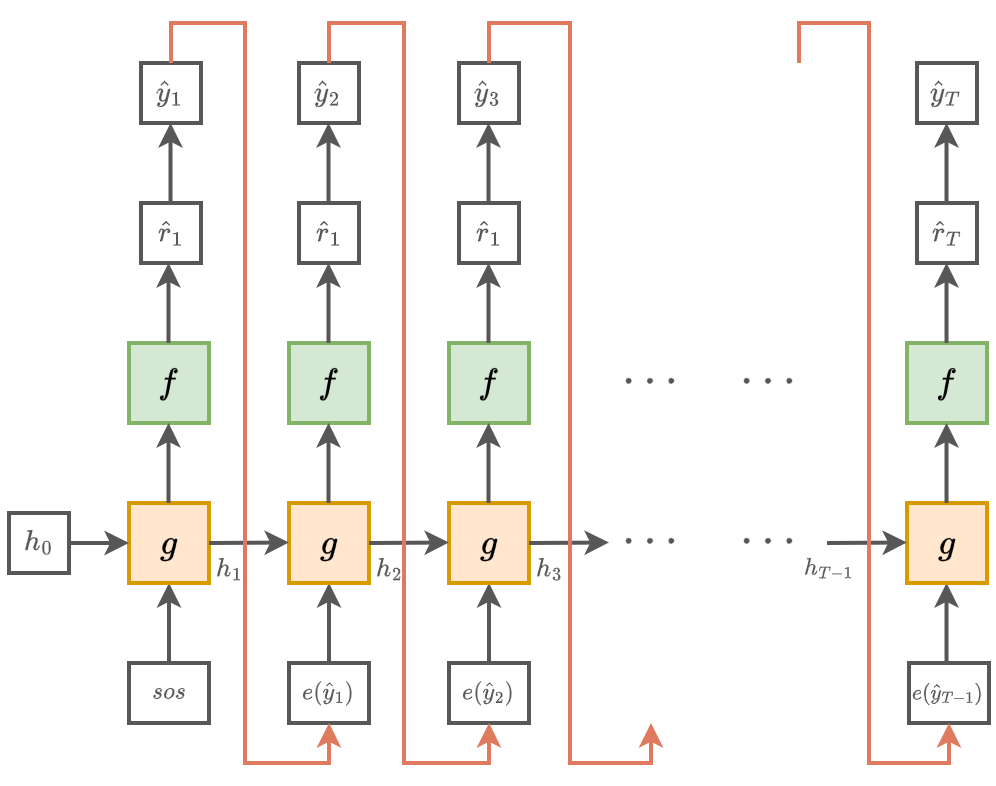
Рассмотрим, как рекуррентная сеть генерирует дискретные объекты на примере генерации текста (как последовательности слов).

Для VV слов в словаре на каждом шаге tt рекуррентная сеть выдаёт VV рейтингов каждого слова:

r^=[r^1,r^2,...r^V]=f(xt,ht)\hat{\mathbf{r}}=[\hat{r}_1,\hat{r}_2,...\hat{r}_V]=f(\mathbf{x}_t, \mathbf{h}_t)

Эти рейтинги преобразуются в вероятности слов с помощью SoftMax-преобразования.

SoftMaxτ(r^1,...r^V)=1∑ier^i/τ⋅(er^1/τer^2/τ⋯er^V/τ),\text{SoftMax}_{\tau}\left(\widehat{r}_{1},...\widehat{r}_{V}\right)=\frac{1}{\sum_{i}e^{\widehat{r}_{i}/\tau}}\cdot\left(\begin{array}{c} e^{\widehat{r}_{1}/\tau}\\ e^{\widehat{r}_{2}/\tau}\\ \cdots\\ e^{\widehat{r}_{V}/\tau} \end{array}\right), τ>0−гиперпараметр температуры.\tau>0 - \text{гиперпараметр температуры.}

  • Во время обучения генерируется самое вероятное слово.

  • Во время применения генерируется самое вероятное слово, либо слово случайно сэмплируется из предсказанного распределения. Варьируя τ\tau, можно управлять противоречием между согласованностью и разнообразием генерируемого текста.

На вход в следующий момент времени подаётся эмбеддинг сгенерированного слова e(y^t)\mathbf{e}\left(\hat{y}_t\right), который можно

  • брать из другой задачи (например, Word2Vec или fastText);

  • настраивать вместе с параметрами рекуррентной сети

    (для больших выборок).

Графически процесс генерации будет выглядеть следующим образом:

Остановка генерации​

Генерацию можно продолжать, пока предсказываемая вероятность остановки pt=s(ht)p_t=s(\mathbf{h}_t) невелика (ниже порога). Альтернативно, и это более частый способ, пока не сгенерируется специальный токен [EOS], означающий конец последовательности (end of sequence).

Обучение генеративной сети​

Генеративная сеть обучается на фрагментах реальных последовательностей y1y2...yT\mathbf{y}_1 \mathbf{y}_2 ... \mathbf{y}_T, где целевыми значениями выступают значения той же последовательности, сдвинутые на единицу: y2y3...yT+1\mathbf{y}_2\mathbf{y}_3...\mathbf{y}_{T+1}, чтобы сеть училась по истории последовательности предсказывать её следующий элемент.

В случае регрессии используются регрессионные функции потерь, а в случае классификации - обычно кросс-энтропийные.

Free run​

Если во время обучения на вход в следующий момент времени подаётся сгенерированный элемент (или его эмбеддинг для дискретных объектов), то такой режим называется free run. Он отвечает реальному применению сети, однако требует более длительного обучения, поскольку сети сложно научиться генерировать правильно всю последовательность целиком.

Teacher forcing​

Сеть будет обучаться существенно проще и быстрее, если ей упростить задачу прогнозирования. А именно, если подавать ей на вход реальные элементы последовательности (их эмбеддинги в дискретном случае) с предыдущего шага, а не те, которые она спрогнозировала. Так задача правильной генерации всей последовательности упрощается до правильного прогнозирования только следующего элемента. Такой режим обучения называется teacher forcing.

Однако в режиме применения сети всё равно придётся генерировать новые последовательности на основе сгенерированных предыдущих. Если она на каком-то шаге сгенерирует неправильный вариант, то ей сложнее будет восстанавливаться и вернуться к правильной траектории генерации, поскольку сеть обучалась только на правильных входах.

Объединение двух стратегий​

Оптимальным с точки зрения скорости обучения и эффективности применения является комбинация двух стратегий одним из способов ниже.

Способ 1:

  1. Обучить в режиме teacher forcing.

  2. Дообучить в режиме free run.

Способ 2:

  • Обучать одновременно в двух режимах, когда на каждом шаге tt с вероятностью pp подаётся реальный вход, а с вероятностью (1−p)(1-p) - сгенерированный.

  • По ходу обучения можно постепенно уменьшать pp до нуля, что будет означать постепенный переход от teacher forcing к free run.

Далее мы изучим, как оценивать качество работы языковых моделей, а также как их применять, чтобы сгенерированные последовательности слов оказывались более естественными, используя лучевой поиск (beam search).

Литература​

  1. http://karpathy.github.io/2015/05/21/rnn-effectiveness/