Ранняя остановка и зашумление входов

Ранняя остановка

Ранняя остановка (early stopping [1]) - другой пример ограничения нейросети, чтобы уменьшить её степень переобучения. Для этого нужно отслеживать потери модели по ходу обучения на валидационной выборке и заранее остановить обучение, когда потери на валидации начнут расти.

На графике ниже нужно остановить обучение сети по достижении пунктирной линии:

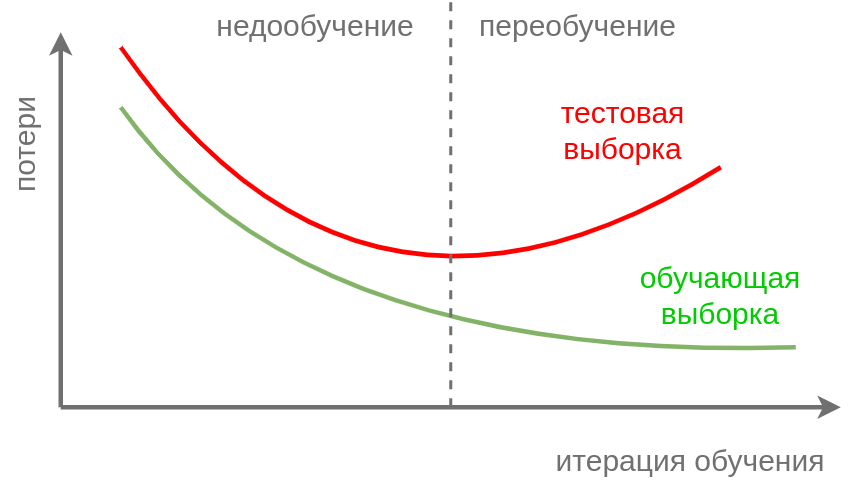
Эта стратегия объясняется тем, что вначале модель учится восстанавливать общую закономерность в данных, а начиная с некоторого момента её обобщающая способность начинает ухудшаться из-за переобучения под конкретную реализацию обучающей выборки.

Поэтому имеет смысл заранее прервать обучение, получив более простую и менее переобученную модель.

Зашумление данных

Другим приёмом упрощения модели служит её обучение на зашумлённых версиях объектов:

$$(\mathbf{x},y) \to (\mathbf{x}+\mathbf{\varepsilon},y),$$

где $\mathbf{\varepsilon}$ - $D$-мерный вектор случайных чисел (случайный шум), обладающий свойствами:

$$\mathbb{E}\mathbf{\varepsilon} = 0, \quad \text{cov}\{\mathbf{\varepsilon}\}=\lambda I,$$

где $I\in\mathbb{R}^{D\times D}$ - единичная матрица. При этом применение модели осуществляется на исходных данных без зашумления.

В [2] доказывается, что обучение регресии $f(\mathbf{x})$, минимизируя MSE-критерий на зашумлённых данных, эквивалентно обучению сети на незашумлённых данных с добавлением следующей регуляризации:

$$\frac{1}{N}\sum_{n=1}^N (f(\mathbf{x}_n)-y_n)^2 + \textcolor{red}{\lambda \| \nabla_\mathbf{x} f(\mathbf{x}) \|^2} \to \min_\mathbf{w}$$

Таким образом, зашумление признаков требует от модели, чтобы изменение её прогнозов было менее резким при небольшом изменении вектора признаков $\mathbf{x}$, что отвечает реальным зависимостям в данных на практике.

В случае, когда $f(\mathbf{x})$ - линейная регрессия, зашумление эквивалентно L2-регуляризации её весов.

Литература

1. Wikipedia: Early stopping.
2. Bishop C. M. Regularization and complexity control in feed-forward networks. – 1995.