DropOut в нейронных сетях

Усредняющий ансамбль

В разделе про ансамбли моделей мы видели, что частым способом упрощения набора переобученных моделей $f_1(\mathbf{x}),...f_M(\mathbf{x})$ является построение усредняющего ансамбля:

$$\hat{y}=\frac{1}{M}\sum_{m=1}^M f_m(\mathbf{x})$$

Задача

Докажите, что мат. ожидание квадрата ошибки усредняющего ансамбля никогда не превосходит среднее мат. ожиданий квадратов ошибок базовых моделей $f_1(\mathbf{x}),...f_M(\mathbf{x})$.

Поскольку нейросети содержат большое число параметров и часто являются переобученными, то их усреднение существенно повышает качество прогнозов. Однако применение усредняющего ансамбля напрямую несёт в себе вычислительные издержки - в $M$ раз увеличиваются расходы на настройку моделей, их хранение и применение, что особенно чувствительно, когда моделями выступают большие и глубокие нейросети.

Дропаут

Эффективным способом моделирования усредняющего ансамбля без сопутствующих издержек является дропаут (DropOut) [1].

Дропаут применяется к определённому слою нейросети, которым может выступать скрытый слой или входной слой (вектор признаков $\mathbf{x}$), но не выходной.

Характер применения дропаута различается при обучении сети (training) и её применении (inference).

Обучение сети

На каждом шаге оптимизации методом обратного распространения ошибки проход вперёд (forward pass) и назад (backward pass) осуществляется не по всей сети, а по её прореженной версии, при которой случайная часть нейронов оставляется, а другая часть - исключается, как показано на примере ниже для скрытого слоя сети:

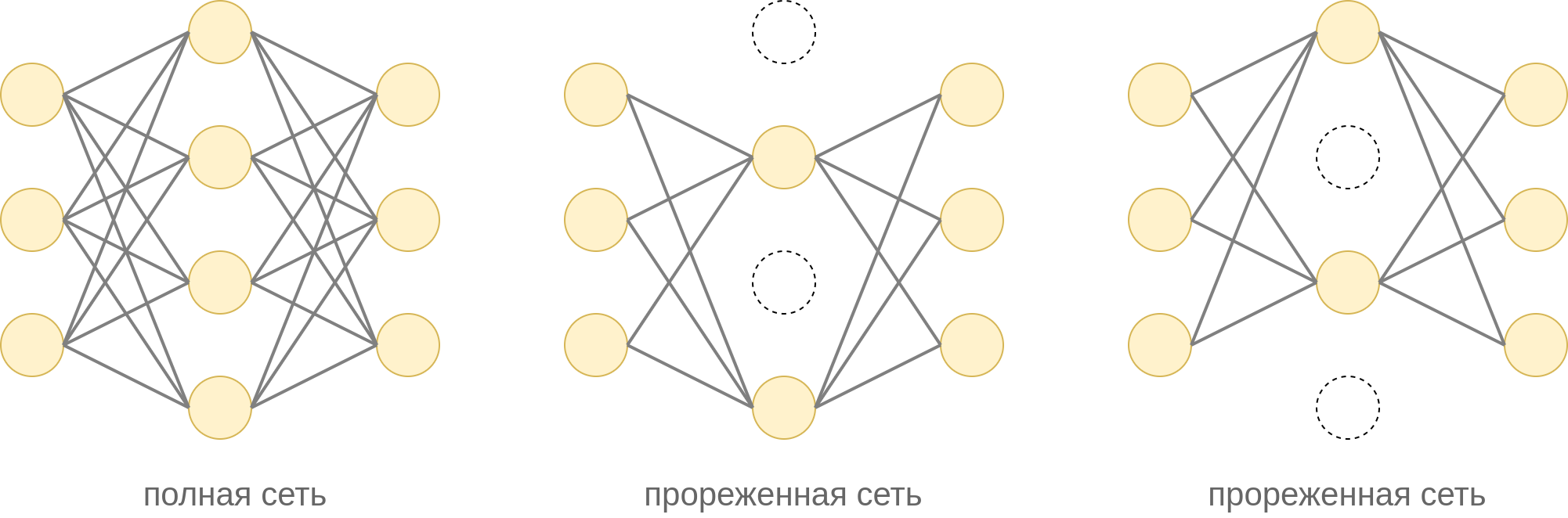
При прореживании каждый нейрон прореживаемого слоя оставляется с вероятностью $p$ и исключается в вероятностью $1-p$ независимо от остальных нейронов.

Гиперпараметр $p$ подбирается по валидационной выборке. Значение по умолчанию $p=0.5$ в общем случае будет неоптимальным. При этом оптимальное значение может быть своим для каждого слоя нейросети.

Исключение нейрона означает, что исключается как сам нейрон, так и все входящие и исходящие из него связи. На практике исключение реализуется домножением весов на матрицу $R$ со случайными элементами из множества $\{0,1\}$.

После прореживания обновление весов для минибатча производится только по оставленным связям.

Если в прореживаемом слое $M$ нейронов, то, по сути, во время обучения настраивается не одна, а целый ансамбль из $2^M$ моделей, представляющих собой различные варианты прореживания полной сети.

По сравнению с настройкой одной полной модели настройка не усложняется, а наоборот упрощается, поскольку проход вперед и назад происходит по облегчённой прореженной версии исходной сети!

Применение настроенной сети

Дропаут Монте-Карло

Теоретически верным построением прогноза для настроенного дропаутом ансамбля моделей будет усреднение по всевозможным вариантам прореживания $R$:

$$\hat{y}(\mathbf{x})=\frac{1}{2^M}\sum_{R}\hat{y}(\mathbf{x}|R),$$

где $\hat{y}(\mathbf{x}|R)$ - прогноз при прореживании $R$, а $\hat{y}(\mathbf{x})$ - итоговый прогноз. На практике усреднение уже по 10-20 случайным маскам $R$ даёт хороший результат. Такая схема применения называется дропаутом Монте-Карло (Monte Carlo dropout).

Достоинством подобного применения DropOut является то, что мы получаем не одно значение прогноза, а сразу несколько, за счёт чего можем оценить стандартное отклонение прогнозов, оценивающее ожидаемую ошибку прогноза. Недостатком является усложнение построения прогноза в $K$ раз, где $K$ - число реализаций прореживания, по которым мы производим усреднение.

Классическое применение

Поскольку усреднение по всевозможным прореживаниям замедляет построение прогнозов, чаще всего применяется классический дропаут, при котором на этапе применения (inference) используются все нейроны (без прореживания), но их активации домножаются на $p$ (вероятность того, что нейрон был оставлен во время обучения).

Это мотивируется следующим. Если $z_1,...z_M$ - выходные активации прореживаемого слоя, то нейрон последующего слоя (во время обучения) принимает на вход

$$a=\sum_{i=1}^M w_i z_i r_i,\quad r_i=\begin{cases} 1, \text{ с вероятностью } p \\ 0, \text{ с вероятностью }1-p \end{cases}$$

Если усреднить по всевозможным реализациям прореживания, то нейрон в среднем будет получать активацию

$$\mathbb{E}_r\left\{a\right\} = \mathbb{E}_r\left\{\sum_{i=1}^M w_i z_i r_i\right\} = \sum_{i=1}^M w_i z_i p$$

Обратим внимание, что для не тождественной активации $g(a)$

$$\mathbb{E}_r g(a) \ne g(\mathbb{E}_r\{a\}),$$

поэтому классический дропаут не эквивалентен усреднению конечных выходов сети по всевозможным прореживаниям. Тем не менее, это приближение наиболее часто используется на практике из-за простоты и скорости построения прогнозов.

Дополнительное ускорение

Слой дропаута при применении сети домножает активации нейронов на $p$, что приводит к дополнительным операциям умножения во время построения прогноза.

Чтобы от них избавиться, можно во время обучения сети делить активации прореживаемых нейронов на $p$. Тогда во время применения никаких умножений на $p$ производить уже не надо!

Особенности применения DropOut

Параметром дропаута выступает вероятность оставления нейрона $p$ при прореживании.

Как влияет вероятность $p$ на сложность нейросети?

Чем $p$ выше, тем в среднем ближе прореженная сеть будет оказываться к полной сети, а следовательно, сеть с дропаутом будет получаться сложнее. Чтобы бороться с переобучением, нужно понизить $p$.

Дропаут можно применять к скрытым слоям и к входному слою (содержащему входной вектор признаков $x$), но не к выходному слою.

Как правило, дропаут применяется не к одному, а сразу к нескольким слоям. Параметр $p$ подбирается по валидационной выборке или кросс-валидации, причём его можно выбирать своим для каждого слоя сети.

Рекомендации по выбору $p$

Общая рекомендация по выбору параметра $p$ заключается в том, чтобы задавать его значение более высоким для начальных слоёв сети и более низким - для более глубоких.

Это связано с тем, что начальные слои содержат ключевую информацию об обрабатываемом объекте (которую нельзя терять), а более глубокие слои - всевозможные высокоуровневые признаки, лишь часть из которых окажется в итоге полезной.

Обоснование метода

Дропаут позволяет контролировать сложность нейросети, осуществляя её регуляризацию.

Он препятствует переобучению в виде чрезмерной сонастройки нейронов на активации друг друга (neuron co-adaptation). Выходные нейроны не могут рассчитывать на активацию отдельного нейрона предыдущего слоя (поскольку он может быть прорежен), поэтому вынуждены использовать информацию со всех доступных нейронов.

Например, при классификации изображений промежуточные нейроны могут детектировать окна машины или её багажник. При переобучении модели машина будет детектироваться только при наличии окон и багажника. Однако реальные машины могут не иметь багажника (хетчбэк) или окон (машина с открытым верхом). Поэтому полагаться только на эти признаки неразумно, а правильнее детектировать машину по всему спектру доступных признаков (наличие дверей, фар, капота, шин и т.д.).

DropConnect

Альтернативным дропауту методом регуляризации сети является метод DropConnect [2], в котором с вероятностью $p$ отбрасываются не нейроны, а отдельные связи на выбранном слое. Два варианта такого прореживания показаны ниже:

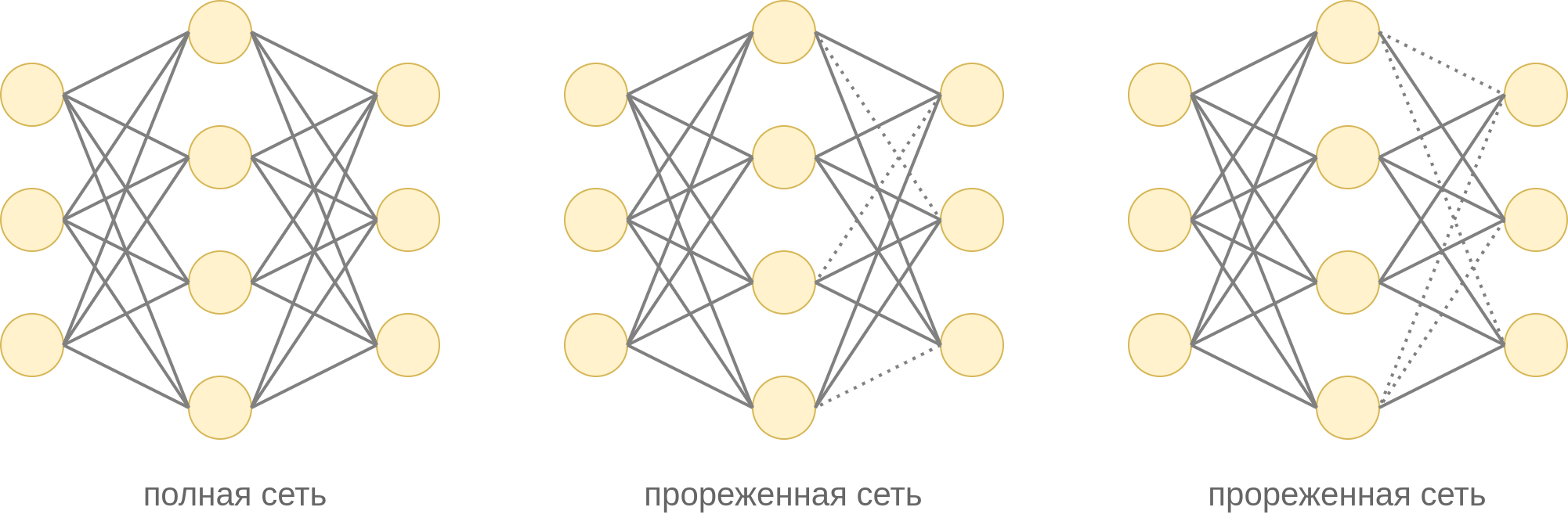
DropConnect по-разному работает в режиме обучения и применения модели аналогично дропауту.

Литература

1. Srivastava N. et al. Dropout: a simple way to prevent neural networks from overfitting //The journal of machine learning research. – 2014. – Т. 15. – №. 1. – С. 1929-1958.
2. Wan L. et al. Regularization of neural networks using dropconnect //International conference on machine learning. – PMLR, 2013. – С. 1058-1066.