Подавление немаксимумов

Базовый алгоритм NMS

Алгоритмы детекции объектов генерируют избыточное количество выделений объектов интересующих классов, как показано на рисунке справа-вверху [1]:

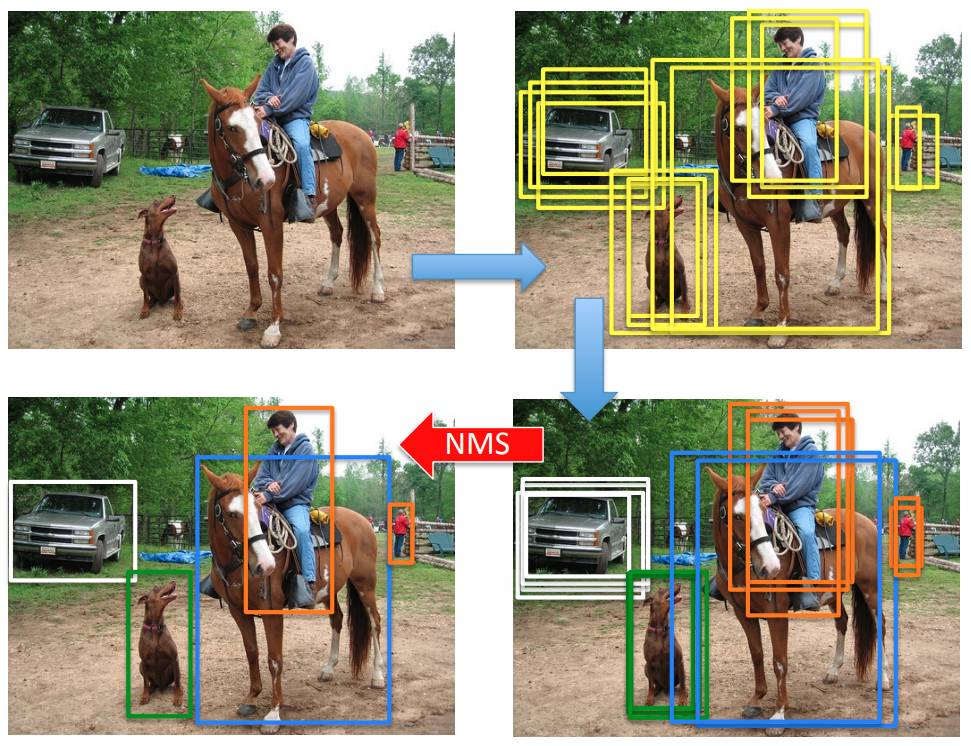
Эти выделения соотносятся тому или иному классу классификатором, назначающим степень принадлежности рамки каждому классу (рейтинг класса). Расположение самого выделения немного уточняется регрессором, как показано справа внизу.

Чтобы отобрать минимально достаточный набор выделений, используется алгоритм подавления немаксимумов (non-maximum supression, NMS), фильтрующий избыточные детекции, имеющие сильное пересечение по мере IoU с другими, обладающими более высоким рейтингом. Он применяется для каждого класса в отдельности.

Алгоритм принимает на вход набор детекций (выделяющих рамок) $B$ и соответствующих рейтингов (вероятностей определённого класса) $S$, а на выходе выдаёт самые явные детекции без повторений $B'$ с соответствующими рейтингами $S$. Он работает следующим образом:

ВХОД:

• $B=\{\mathbf{b}_1,...\mathbf{b}_N\}$ - первоначальные детекции

• $S=\{s_1,...s_N\}$ - их рейтинги

• $\alpha\in (0,1]$ - гиперпараметр NMS

АЛГОРИТМ:

• $B'=\{\}$ - инициализируем выходные детекции

• $S'=\{\}$ - инициализируем выходные рейтинги

• пока $B\ne \{\}$:

  • $m:=\arg\max S$

  • $B':=B'+ \{\mathbf{b}_m\}$

  • $B:=B-\{\mathbf{b}_m\}$

  • для $\mathbf{b}_i \in B$:

    • если $\text{IoU}(\mathbf{b}_m,\mathbf{b}_i)\ge \alpha$, то

      • $B:=B-\{\mathbf{b}_i\}$

      • $S:=S-\{s_i\}$

• вернуть $B',S$

где прибавление/вычитание элемента из набора означает добавление/исключение этого элемента из множества.

Мягкий вариант алгоритма NMS

Базовый алгоритм подавления немаксимумов жёстко отбрасывает выделения, имеющие IoU$\ge\alpha$ с другим выделением, имеющим более высокий рейтинг. Это может негативно сказаться на количестве обнаруженных объектов (recall), которые сильно пересекаются, как на рисунке ниже:

Для того, чтобы этого не происходило, в работе [1] предлагается оставлять все детекции, но для выделений, имеющих сильное пересечение с другими высокорейтинговыми выделениями, дополнительно снижать рейтинг. Итоговыми детекциями будут те, у которых рейтинг выше некоторого порога $\beta>0$, устанавливая который достаточно низким, можно извлечь большее число объектов (ценой более частых дублированных выделений одного и того же объекта).

Этот алгоритм называется мягким подавлением немаксимумов (soft-NMS) и работает следующим образом:

ВХОД:

• $B=\{\mathbf{b}_1,...\mathbf{b}_N\}$ - первоначальные детекции

• $S=\{s_1,...s_N\}$ - их рейтинги

• $\alpha\in (0,1]$ - гиперпараметр NMS

АЛГОРИТМ:

• $B'=\{\}$ - инициализируем выходные детекции

• пока $B\ne \{\}$:

  • $m:=\arg\max S$

  • $B':=B'+\{\mathbf{b}_m\}$

  • $B:=B-\{\mathbf{b}_m\}$

  • для $b_i \in B$:

    • $s_i:=s_i\cdot f(\text{IoU}(\mathbf{b}_m,\mathbf{b}_i))$

• вернуть $D,S$

Как видим, в качестве $\mathbf{b}_m$ в этот раз перебираются все детекции из $B$, в результате чего $B'=B$, т.е. выходные детекции совпадают со всеми входными, однако рейтинг детекций, имеющих сильное пересечение с другими высокорейтинговыми выделениями, оказывается сниженным за счёт домножения исходного рейтинга на $f(\text{IoU}(\mathbf{b}_m,\mathbf{b}_i))$ для некоторой убывающей функции $f(\cdot)$, принимающей значения на отрезке $[0,1]$. Предлагаются два варианта этой функции:

• линейное перевзвешивание:

$$f(\text{IoU}(b_m,b_i))= \begin{cases} 1, & \text{IoU}(\mathbf{b}_m,\mathbf{b}_i)<\alpha, \\ 1-\text{IoU}(\mathbf{b}_m,\mathbf{b}_i), & \text{IoU}(\mathbf{b}_m,\mathbf{b}_i)\ge\alpha \\ \end{cases}$$

• Гауссово перевзвешивание:

  $$f(\text{IoU}(\mathbf{b}_m,\mathbf{b}_i))=e^{-\frac{\text{IoU}(\mathbf{b}_m,\mathbf{b}_i)}{\sigma}},\quad \sigma>0 \text{ - гиперпараметр}$$

Линейное перевзвешивание приводит к разрывному масштабированию, в отличие от Гауссова. В экспериментах [1] мягкое подавление немаксимумов оказалось лучше, чем жёсткое. При этом иногда доминировало линейное, а иногда - Гауссово перевзвешивание.

Литература

1. Bodla N. et al. Soft-NMS--improving object detection with one line of code //Proceedings of the IEEE international conference on computer vision. – 2017. – С. 5561-5569.