Меры качества прогнозов

Изучим основные меры качества прогнозов семантической сегментации.

Рассмотрим семантическую сегментацию на два класса - целевой объект и фон.

Целевым объектом может быть человек на фотографии, заболевание на рентгеновском снимке и т.д.

Попиксельная точность

Самой простой мерой качества сегментации является попиксельная точность (pixel accuracy), т.е. доля верно классифицированных пикселей. Недостатком этой меры является завышенное качество, когда фон доминирует над целевым классом, что является типичной ситуацией. В этом случае модель будет показывать высокую точность, даже если модель не будет решать задачу, а все пиксели будет относить к фону!

IoU и Dice

Нам нужна мера, которая бы вычисляла качество предсказания именно целевого класса. Самой популярной мерой является мера Жаккара, в компьютерном зрении называемая Intersection-over-Union или IoU.

Пусть

$Y$ - множество пикселей, реально принадлежащих целевому классу,
$\hat{Y}$ - множество пикселей, отнесённых моделью к целевому классу.

Тогда качество выделения целевого класса считается как

\text{IoU}=\frac{|\hat{Y} \cap Y|}{|\hat{Y} \cup Y|},

что графически можно представить следующим образом:

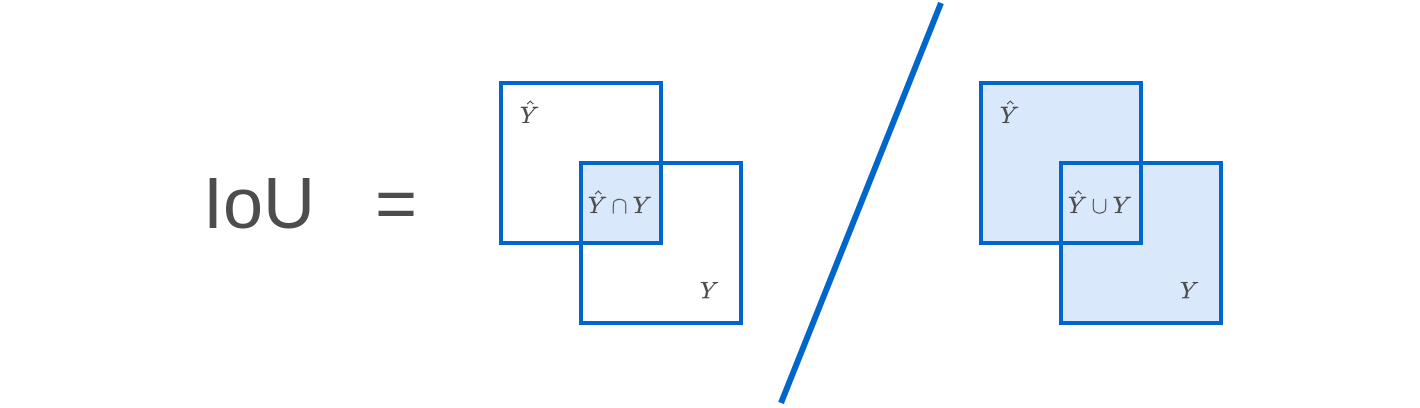
Также популярна мера качества Dice:

\text{Dice}=\frac{2|\widehat{Y}\cap Y|}{|\widehat{Y}|+|Y|},

которая графически выглядит как

Из определения следует, что обе меры принимают значения из отрезка [0,1], причём

1 соответствует наилучшей сегментации (множества совпали),
0 соответствует наихудшей сегментации (множества не имеют пересечения).

Если целевой класс обозначить положительным, а фон - отрицательным классом, то в терминах величин TP, TN, FP, FN эти меры запишутся как

\text{IoU} = \frac{TP}{TP+FP+FN},

\text{Dice}=\frac{2TP}{2TP+FP+FN}=\frac{1}{\frac{1}{2}\frac{\widehat{P}}{TP}+\frac{1}{2}\frac{P}{TP}}=\text{F-мера},

где

$\hat{P}=TP+FP$ - число предсказаний целевого класса,
$P=TP+FN$ - число реальных пикселей целевого класса.

Поскольку в Dice, по сравнению с IoU, и в числителе, и в знаменателе прибавляется величина TP, то Dice будет выдавать более высокие значения для в целом верно распознанных регионов целевого класса:

\text{Dice}=\frac{{\color{red}{\color{green}{\color{green}TP}+}TP}}{{\color{green}TP+}{\color{red}TP+FP+FN}}

По смыслу меры IoU и Dice измеряют одно и то же (качество выделения целевого класса) и связаны монотонным соотношением (докажите!):

Dice=\frac{2IoU}{IoU+1}

Сглаженные варианты IoU и Dice

Поскольку сегментационная модель выдаёт не сами классы, а их вероятности, то имеет смысл обобщить меры IoU и Dice на оценку предсказываемых вероятностей, как показано на рисунке [1]:

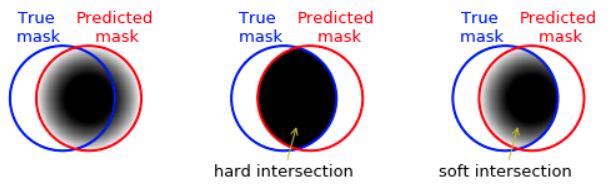
Пусть теперь

$Y\in \mathbb{R}^{H,W}$ - матрица истинной разметки, в которой 1 стоит в пикселях целевого класса, а 0 обозначает фон;
$P\in\mathbb{R}^{H\times W}$ - матрица, каждый элемент которой задаёт предсказанную вероятность целевого класса в каждом пикселе.

Тогда меру IoU можно применять как [2]:

\text{IoU}_{soft}^1 = \frac{\langle Y,P\rangle}{||Y||_1+||P||_1-\langle Y,P \rangle},

\text{IoU}_{soft}^2 = \frac{\langle Y,P\rangle}{||Y||_2^2+||P||_2^2-\langle Y,P \rangle},

а меру Dice как

\text{Dice}_{soft}^1 = \frac{2\langle Y,P\rangle}{||Y||_1+||P||_1},

\text{Dice}_{soft}^2 = \frac{2\langle Y,P\rangle}{||Y||_2^2+||P||_2^2}

Преимуществом подобных мер является то, что они дифференцируемы по вероятностям, следовательно можно не только отслеживать по ним качество прогнозов, но и использовать их напрямую в настройке параметров модели как целевые критерии оптимизации.

В работе [2] рассматриваются и другие меры обобщения IoU на случай вероятностных прогнозов.

Пограничная IoU

Часто модель сегментации хорошо справляется с выделением объекта в целом, а большая часть ошибок концентрируется на границах объектов. Для детальной оценки качества сегментации именно на границах IoU применяется не по всему изображению, а только вдоль границ объектов.

Пусть

$B_{r}(Y)$ - полоса ширины $r$ вокруг границы реальной маски $Y$ .
$B_{r}(\hat{Y})$ - полоса ширины $r$ вокруг границы предсказанной маски $\hat{Y}$ .

Тогда качество вдоль границ объектов можно оценивать одним из следующих способов [3]:

\text{Trimap IoU}=\frac{\left|{\color{red}B_{r}(Y)\cap}\widehat{Y}\cap Y\right|}{\left|\left({\color{red}B_{r}(Y)\cap}\widehat{Y}\right)\cup\left({\color{red}B_{r}(Y)\cap}Y\right)\right|}

\text{Boundary IoU}=\frac{\left|\left({\color{red}B_{r}(\widehat{Y})\cap}\widehat{Y}\right)\cap\left({\color{red}B_{r}(Y)\cap}Y\right)\right|}{\left|\left({\color{red}B_{r}(\widehat{Y})\cap}\widehat{Y}\right)\cup\left({\color{red}B_{r}(Y)\cap}Y\right)\right|}

Average Precision

Можно варьировать порог вероятности $\alpha$ , начиная с которого пикселю будет назначаться целевой класс (а не фон):

p(i,j)\ge \alpha \Longrightarrow \; \hat{y} \; (i,j)=1

При более низком пороге целевой класс будет назначаться более часто.

При варьировании $\alpha$ будут изменяться меры Precision и Recall.

Агрегированной мерой качества сегментатора для различных порогов будет кривая зависимости Precision(Recall) при различных порогах $\alpha$ , известная как кривая точности-полноты (precision-recall curve).

Пример этой кривой показан ниже [4]:

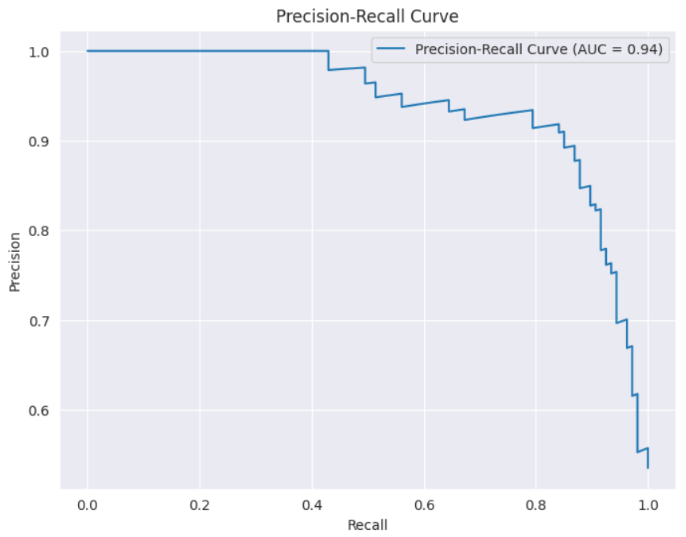
Агрегированной численной мерой качества для всевозможных порогов будет величина Average precision (AP), равная площади под графиком зависимости точности от полноты.

Случай многих классов

Если производится сегментация на $C$ классов, то оценивают качества выделения каждого класса одной из вышеприведённых мер, а затем меры для каждого класса усредняют. Величина Average Precision, равномерно усреднённая по классам, называется Mean Average Precision (mAP).

Меры качества прогнозов

Попиксельная точность​

IoU и Dice​

Сглаженные варианты IoU и Dice​

Пограничная IoU​

Average Precision​

Случай многих классов​

Литература​